Hôm nay, 19/01/2015, tôi bắt đầu dạy môn PTĐHR cho lớp K57A1T và K57TN. Giáo trình tôi sử dụng
“Giáo trình PTĐHR” của thầy Nguyễn Thừa Hợp.
Ngoài ra tôi còn sử dụng thêm các giáo trình:
+”An introduction to PDEs” của Y. Pinchover và J. Rubinstein;
+”Methods of Applỉed Mathematics III: PDEs” của Bernard Deconinck.
Sách của thầy Hợp các bạn có thể mượn thư viện.
Cuốn của Pinchover và Rubinstein các bạn có thể tìm trong bài
https://bomongiaitich.wordpress.com/2014/02/10/trao-doi-bai-giang-mon-ptdhr-lop-k56a1t/
Giáo trình của giáo sư Bernard các bạn có tìm trong trang
http://depts.washington.edu/bdecon/bernard/
Có gì cần trao đổi các bạn có thể viết vào phần “Phản hồi”.
Phần phương pháp Fokas tôi sử dụng tài liệu khác của giáo sư Bernard
Click to access linear_pde.pdf
Một số lỗi trong cuốn “An introduction to PDEs” của Y. Pinchover, J. Rubinstein
Click to access PDE.pdf
Chẳng hạn phương trình trong bài 2.20, trang 61 cần sửa lại thành
Hay phương trình trong bài 3.6, trang 74 cần sửa lại thành
Danh sách nhóm bài tập lớp K57A1T
Còn hai bạn Đỗ Thị Hiên, Nguyễn Đặng Thanh Hương tôi chưa biết xếp vào nhóm nào.
Ngoài ra, trong nhóm 4 có tên Nguyễn Thị Diệu Hương không có trong danh sách lớp.
Các bạn chưa tham gia nhóm nào:
Hoàng Tuấn Anh, Nguyễn Thị Quỳnh Anh, Trịnh Kim Chi, Hoàng Trung Dũng, Phạm Xuân Lộc, Tô Thị Ngọc Mai, Đỗ Thu Ngà, Mai Thanh Quang.
Tôi nhầm: bạn Mai Thanh Quang có trong nhóm 7.
Bạn Khuất Đắc Thành chưa tham gia nhóm nào.
thưa thầy, em là nhóm trưởng nhóm 7. Hiện tại, nhóm em có 5 người và có 1 bạn mới đăng kí xin vào nhóm. Vậy thầy có thể cho bạn ấy vào nhóm em được không ạ?? Bạn ấy tên Tô Thị Thu Hằng, mã sv 11001504, lớp k56a1T1
Nếu các bạn đã đồng ý thì được. Chú ý: tham gia vào nhóm không chỉ đơn giản điền tiên vào cho vui.
Bài tập phần phương pháp đặc trưng cho lớp K57A1T
Tôi có dùng thêm cuốn
“PDEs with Fourier series and BVPs” của N. K. Asmar.
Đường link của cuốn sách
https://app.box.com/shared/3x3o35lvuu
Em chào thầy. Thầy ơi bài tập nhóm nộp vào thứ 2 hay thứ 4 tuần sau ạ. Với bài tập ở sách Pinchorver phần c) là ở trang nào ạ
Bài tập phần phương pháp đặc trưng hạn nộp cuối sáng 12/02/2015. Bài tập phần c trang 93 đến 97.
File điện tử của giáo trình của GS. Bernard
https://docs.google.com/file/d/0B257UW6wJ3euMjk2NWM1YWUtMWYyMS00NjM4LWFiYWItZTExNTM2YjdhMmU3/edit?hl=en&pli=1
thưa Thầy, em là Trần Xuân Vinh, sv lớp k55a1t, em đang học môn ptdhr của Thầy học lỳ này, e có đăng ký là thành viên nhóm 7, sao không có tên e trong danh sách nhóm mà thầy đăng lên ạ!
Danh sách các nhóm bài tập sau khi chỉnh sửa
– bạn Trần Xuân Vinh ở nhóm 7,
– nhóm 4 có bạn Phạm Thị Diệu Hương
và bổ sung
– các bạn Nguyễn Thị Diệp, Phạm Thị Thắm tham gia vào nhóm 1,
– bạn Nguyễn Đặng Thanh Hương tham gia vào nhóm 5,
– bạn Đỗ Thị Hiên tham gia vào nhóm 6.
28/01/215 một số bạn làm bài
Một bạn chuyển về dạng chính tắc bằng cách đổi biến
được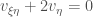 .
.
Kết quả này chưa đúng. Nó dẫn đến việc giải sai các phần tiếp theo
– tìm nghiệm tổng quát,
– (bài toán Goursat) tìm nghiệm riêng khi biết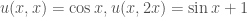 ,
,
– tìm nghiệm tổng quát của phương trình không thuần nhất
Trước khi sửa lại, ta cùng thấy một bài học nhỏ:
Việc giải bài toán qua từng bước như trên, chỉ cần sai một chỗ nhỏ sẽ làm cho bài giải sai từ chỗ đó trở đi.
Quay trở lại việc sửa lại, phương trình dạng chính tắc cần tìm
hay
Nghiệm tổng quát của phương trình thuần nhất
hay
Tiếp tục giải bài toán Goursat, thay nghiệm tổng quát vào điều kiện
Vậy nghiệm của bài toán Goursat
Cuối cùng giải phương trình không thuần nhất. Dạng chính tắc, vẫn dùng phép đổi biến trên,
Vậy nghiệm tổng quát của phương trình không thuần nhất
hây
Không khó để thấy hàm
là một nghiệm riêng của phương trình không thuần nhất.
thưa thầy e hỏi ak!khi giải bài toán Goursat, thay nghiệm tổng quát vào điều kiện thì ta luôn có F(0)+G(0)=1 ak?thầy giải thích giúp e vs ak.e cảm ơn thầy!
Điều này phụ thuộc vào từng bài. Chẳng hạn trong bài này ta lấy x=0 thay vào các điều kiện ta có
em thưa thầy , đề thi giữa kì chúng em sưu tầm ở đâu ạ? thầy có thể đưa lên cho chúng em được không ạ?
Em vào chuyên mục “Đề thi”
https://bomongiaitich.wordpress.com/category/d%E1%BB%81-thi/
Sau đó chọn bài nào ứng với từng đề thi, chẳng hạn đề thi giữa kỳ K57A1C
https://bomongiaitich.wordpress.com/2014/11/06/de-thi-giua-ky-mon-ptdhr-k57a1c/
Nháy chuột vào ngay dòng đầu của bài sẽ ra file đề thi, chẳng hạn
Click to access dethigiuakyk57a1cn1.pdf
dạ vâng. em cảm ơn thầy
thưa thầy!vậy như câu c,(GKK54 A2-DD6-B1),khi thay nghiệm tổng quát vào đk e đc F(4x)+G(0)=cos(2x) và e^(-x).F(0)+G(4x)=-e^(-2x)sinx.lúc này ko có F(0)+G(0)=1.thì phải giải tiếp thế nào ak?
Câu c bài này: vô nghiệm vì
u(0, 0) vừa bằng 1 vừa bằng 0.
Nếu muốn câu này có nghiệm cần sửa lại chẳng hạn
Nghiệm tổng quát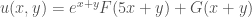 .
.
Khi đó ,
,
Thay ngược lại công thức nghiệm tổng quát ta sẽ tìm được nghiệm.
thưa thầy!thầy xem giúp e đề bài 3.8,sách Y.Pinchover có bị sai đề ko ak
với lại thầy gợi ý giúp e đề GKK56-DD1-B2 vs ak
Tôi đã thử giải và chưa thấy gì sai. Phương trình đặc trưng, phép đổi biến và dạng chính tắc em tính được như nào?
Để làm Bài 2, đề 1 giữa kỳ của K56A1, em thác triển lẻ điều kiện ban đầu rồi dùng công thức D’Alembert tính sóng tiến, sóng lùi. Từ đó vẽ đồ thị nhờ dịch chuyển các sóng này.
em thưa thầy , thầy dịch giúp em đề bài bài (a)5,11 trong sách Asmar được không ạ?
Từ bài 1 đến 8 yêu cầu dùng công thức D’Alembert (4), trang 126, để giải bài toán (1)-(3), trang 126, dao động của sợi dây có độ dài một. Trong công thức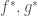 là các thác triển lẻ, tuần hoàn chu kỳ 2 của f, g. Hãy mô tả chi tiết các thác triển này. Riêng bài 5, hàm f được cho như bài 5, mục 3.3 Exerices, trang 123.
là các thác triển lẻ, tuần hoàn chu kỳ 2 của f, g. Hãy mô tả chi tiết các thác triển này. Riêng bài 5, hàm f được cho như bài 5, mục 3.3 Exerices, trang 123.
Bài 11 yêu cầu vẽ đồ thị nghiệm u(x, t) tại các thời điểm t=1/2 và t=1.
phương trình đặc trưng của e là 4y^2(dy)^2-2(1-y^2)dxdy-(dx)^2=0;delta=(2+2y^2)^2>0 là dạng hypecbol,e đặt si=-x+(2/3)y^3;eta=x+2y
sau đó e tìm ra dạng chính tắc dài lắm ak,thầy xem gips e vs
Em đổi biến đúng. Dạng chính tắc tôi tính
e xem lại rồi ak.em bị nhầm dấu ak.e cảm ơn thầy
thưa thầy!thầy có thể nói cho em biết khi nào thì dùng thác triển lẻ,thác triển chẵn và mục đích sử dụng nó vs ak?e vẫn còn mơ hồ về phần đấy ak
Em xem bài này
https://bomongiaitich.wordpress.com/2010/04/13/ph%C6%B0%C6%A1ng-phap-d-alembert-gi%E1%BA%A3i-bai-toan-bien-h%E1%BB%97n-h%E1%BB%A3p-cho-pt-truy%E1%BB%81n-song/
02/02/2015, một bạn lên chữa bài 6/Exercises 3.4, trang 133, trong sách của N. K. Asmar như sau.
Sử dụng công thức D’Alembert giải bài toán biên hỗn hợp cho phương trình
với điều kiện biên Dirichlet thuần nhất
và điều kiện ban đầu
Công thức D’Alembert được sử dụng ở dạng
trong đó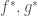 là các thác triển lẻ (vì điều kiện biên Dirichlet thuần nhất), tuần hoàn chu kỳ 2 (hai lần chiều dài).
là các thác triển lẻ (vì điều kiện biên Dirichlet thuần nhất), tuần hoàn chu kỳ 2 (hai lần chiều dài).
Do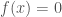 khi
khi 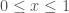 nên
nên  khi
khi 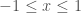 . Tiếp tục thác triển tuần hoàn chu kỳ 2 ta có
. Tiếp tục thác triển tuần hoàn chu kỳ 2 ta có
Với hàm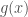 , quá trình thác triển phức tạp hơn một chút như sau:
, quá trình thác triển phức tạp hơn một chút như sau:
– thác triển lẻ:
– thác triển tuần hoàn chu kỳ 2:
khi thì
thì 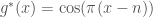 .
.
Nhìn lại công thức D'Alembert, nghiệm của bài toán
với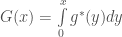 .
.
Để ý rằng nên
nên
hay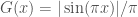 .
.
Vậy nghiệm của bài toán
Một vài hình ảnh:
– thác triển trạng thái ban đầu
– thác triển vận tốc ban đầu, tính “nguyên hàm” của nó
– sóng tại một vài thời điểm
“Nguyên hàm” không phải là nguyên hàm theo nghĩa thông thường của hàm
không phải là nguyên hàm theo nghĩa thông thường của hàm 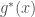 trên toàn trục số, vì nó không khả vi tại các điểm nguyên. Nói cách khác
trên toàn trục số, vì nó không khả vi tại các điểm nguyên. Nói cách khác  có đạo hàm hầu khắp nơi là hàm
có đạo hàm hầu khắp nơi là hàm 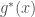 . Điều này dẫn đến nghiệm
. Điều này dẫn đến nghiệm  sẽ không có đạo hàm riêng theo
sẽ không có đạo hàm riêng theo  tại các điểm thuộc đúng một đường đặc trưng dạng
tại các điểm thuộc đúng một đường đặc trưng dạng
hay
Để tìm hiểu thêm vấn đề này các bạn tham khảo bài
https://bomongiaitich.wordpress.com/2014/10/18/tinh-chat-cua-nghiem-phuong-trinh-truyen-song-di-truyen-tu-dieu-kien-ban-dau-2/
Chẳng hạn tại thời điểm nghiệm
nghiệm 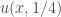 không có đạo hàm riêng theo
không có đạo hàm riêng theo  tại
tại 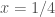 và
và 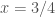 . Như vậy nghiệm tìm được từ công thức D’Alembert không phải là nghiệm cổ điển (classical solution) của bài toán đã cho. Cũng cần lưu ý tại điểm (1/2, 1/2) là điểm thuộc hai đường đặc trưng
. Như vậy nghiệm tìm được từ công thức D’Alembert không phải là nghiệm cổ điển (classical solution) của bài toán đã cho. Cũng cần lưu ý tại điểm (1/2, 1/2) là điểm thuộc hai đường đặc trưng
nghiệm có các đạo hàm riêng
có các đạo hàm riêng
Trở lại vấn đề đầu, hàm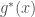 là đạo hàm hầu khắp nơi của hàm
là đạo hàm hầu khắp nơi của hàm  . Về tính chất của hàm
. Về tính chất của hàm  các bạn có thể tham khảo bài
các bạn có thể tham khảo bài
https://bomongiaitich.wordpress.com/2014/09/12/tinh-lien-tuc-tuyet-doi-cua-nguyen-ham-ham-kha-tich-lebesgue/
hay luận văn của Vũ Công Viên
Click to access luan_van.pdf
thưa thầy, em tìm được dạng chính tắc v_ηη+v_η=0 . Vậy giờ làm thế nào để tìm nghiệm tổng quát ạ?
Khi đó
Tiếp tục tích phân dần lên sẽ thu được nghiệm tổng quát.
Tôi vừa nhận được danh sách mới. Trong danh sách mới:
– các bạn Phan Phương Đức (K54TT) và Võ Duy Hoàng (K55TT) chưa tham gia nhóm nào,
– bạn Tô Thị Thu Hằng tham gia vào nhóm 7,
– bạn Nguyễn Đặng Thanh Hương (nhóm 5) không có tên trong danh sách mới,
– bạn Nguyễn Phương Dung, Đỗ Thu Ngà, Dương Minh Tân chưa tham gia nhóm nào.
Thưa thầy , cho em được hỏi bài 2.20 trang 61 sách của Pinchover câu d chứng minh w1(w2-w3) bằng không là em làm với các hàm x,y,u tổng quát ở câu a hay bài toán Cauchy ở câu b có thêm điều kiện u(s,s) = -2s ạ .
Em xin cảm ơn .
x, y, u chỉ thoả mãn phương trình. Chú ý phương trình của bài này cần sửa lại
thầy giải giúp e bài Gk-k56TT-Đ1-B2 với ạ
Em thác triển lẻ các điều kiện ban đầu (tại sao?) thu được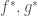 .
.
Tiếp đến tìm “nguyên hàm”
Lắp vào công thức tính
sóng tiến ,
,
sóng lùi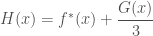 .
.
Khi đó nghiệm
Về cơ bản nó khá giống bài
https://bomongiaitich.wordpress.com/2013/01/30/bai-tap-su-dung-do-thi-giai-nghiem-cho-bai-toan-cauchy/
với hình ảnh
Click to access anh-tuan.pdf
Thưa thầy em là Dương Minh Tân,lớp K57A1T1.Thầy xem lại giúp em với ạ,em thuộc nhóm 7 chứ không phải chưa có nhóm. Em cảm ơn thầy ạ.
Tôi xin lỗi. Dương Minh Tân có trong nhóm 7.
thầy dịch giúp e bài 4.11 trong sách pinchorver với ạ
Áp suất P(x, t) sinh ra từ một vụ nổ thoả mãn bài toán giá trị ban đầu như đề ra. Một toà nhà ở vị trí x_0=10, có thể chịu được áp suất P=6.
Tìm thời điểm t_0 mà áp suất P(10, t) đạt giá trị lớn nhất. Hỏi toà nhà có bị sập không?
em thưa thầy, thầy giúp em bài 5/133 sách Asmar với ạ. f(x) có 2 giá trị nên em không biết làm thế nào ạ?
Không phải f(x) có hai giá trị mà trên từng khoảng nó được cho bởi các công thức khác nhau. Em vẽ đồ thị f(x) rồi thác triển lẻ, tuần hoàn chu kỳ 2 sẽ nhìn được f^*(x). Thế em thác triển hàm g(x) như nào?
em thưa thầy, hàm g(x) em thác triển :g*(x) = x ạ
Tôi đã nghĩ em sẽ làm như vậy. Em quên mất g^* tuần hoàn chu kỳ 2. Nếu g^*(x)=x thì nó không tuần hoàn. Kết quả này chỉ đúng trong một chu kỳ, nghĩa là
g^*(x)=x khi -1<x<1.
Em mới chỉ thác triển lẻ. Tiếp đến thác triển tuần hoàn chu kỳ 2.
Em xem lại bài 6/Exercises 3.4, tôi đã viết qua cách làm ở trên.
thưa thầy hàm g*(x) =x-2n với n thuộc Z phải không ạ?
Còn x nằm ở đâu? Trong trường hợp -1<x<1 ứng với n=0.
Sau đó tính “nguyên hàm” của g^*, chẳng hạn
Cũng giống bài 6/Exercises 3.4, chú ý
thưa thầy là 2n-1 =<x<2n+1 ạ
G(x) = 1/2.(x^(2)-1) nếu -1<x<1 và G(x)= G(x+2) còn lại ạ
Thế còn hàm f^*?
Có thể viết
em vẽ hình ra thi em thấy f*(x)=2x-2n với n=<x<n+1/2 và f*(x)=2(n+1-x) với n+1/2+<x<n+1 ạ
Em chưa thác triển lẻ f(x)? Từ công thức em viết
f^*(x)=-2x khi -1/2<x<0 là chưa đúng!
thưa thầy f*(x)=2x-4n với 2n-1/2 =<x< 2n+1/2
và f*(x) = 2(2n+1-x) với 2n+1/2 =<x<2n+3/2 ạ
Đúng rồi. Vậy nghiệm u(x, t)=?
thưa thầy, vậy em thay cả 2 f* vào thì e được 2 nghiệm ạ?
Một cách tường minh như bài 6/Exercises 3.4 như trên? Chú ý công thức D’Alembert cho ta nghiệm
Ta cũng có thể viết dưới dạng sóng tiến, sóng lùi
với
sóng tiến ,
,
sóng lùi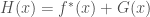 .
.
dạ vâng , em cảm ơn thầy
Thưa thầy cho e hỏi bài 4.15 của rubinstein là phương trình bậc ba . thầy có thể hướng dẫn e với ạ.
và phần b bài 4.5 của rubinstein yêu cầu vẽ hình thì làm thế nào ạ.
Bài 4.15: Em đặt w=u_x thì w thỏa mãn bài toán giá trị ban đầu cho phương trình truyền sóng.
Bài 4.5: Em tính sóng tiến (forward) F(x), sóng lùi (backward) H(x) như câu a yêu cầu. Sau đó từ công thức
u(x, i)=F(x-i)+G(x+i)
em vẽ đồ thị của u(x, i), i=4, 8, 12 nhờ việc dịch chuyển đồ thị F(x) sang phải i đơn vị, G(x) sang trái i đơn vị, rồi cộng chúng lại.
Thầy ơi thầy gợi ý giúp em bài 13 trang 133 sách N.K.Asmar với ạ. Giả sử cả 2 hàm f và g đều đối xứng với tâm x=L/2,nghĩa là f(L-x)=f(x) và g(L-x)=g(x).Chứng minh rằng: U(x,t+L/c)= -U(x,t).
Em xem các thác triển lẻ, tuần hoàn chu kỳ 2L f^*, g^* của các hàm f, g có tính chất gì từ tính đối xứng của f, g. Từ đó xem nguyên hàm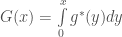 có tính chất gì. Cuối cùng dùng công thức (6) trang 128 sẽ có điều phải chứng minh.
có tính chất gì. Cuối cùng dùng công thức (6) trang 128 sẽ có điều phải chứng minh.
11/02/2015, một số bạn chữa bài 2.3/trang 58, trong sách của Pinchover-Rubinstein. Đề bài xét phương trình
Câu a yêu cầu viết các đường đặc trưng, nghĩa là các đường trong không gian 3-chiều thỏa mãn
Giải hệ này ta được họ các đường đặc trưng
với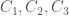 là các hằng số.
là các hằng số.
Câu b, với , yêu cầu tìm một nghiệm hiển thỏa mãn
, yêu cầu tìm một nghiệm hiển thỏa mãn 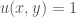 khi
khi 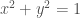 .
.
Tham số số đường tròn bởi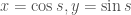 thì
thì  . Ta cần tìm
. Ta cần tìm  tại mỗi điểm
tại mỗi điểm 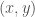 . Đường đặc trưng đi qua
. Đường đặc trưng đi qua 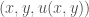 có thời điểm ban đầu xuất phát trên
có thời điểm ban đầu xuất phát trên 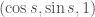 là đường
là đường
Có thể thấy ngay một nghiệm .
.
Câu c, với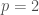 , yêu cầu tìm hai nghiệm thỏa mãn
, yêu cầu tìm hai nghiệm thỏa mãn  . Một bạn đã “mò” được hai nghiệm
. Một bạn đã “mò” được hai nghiệm 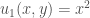 và
và 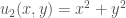 . Tôi có hỏi về lý do, rất may cuối giờ có một bạn lên cho tôi cách tìm: ta lấy thêm điều kiện khác! Chẳng hạn:
. Tôi có hỏi về lý do, rất may cuối giờ có một bạn lên cho tôi cách tìm: ta lấy thêm điều kiện khác! Chẳng hạn:
C1: lấy điều kiện như câu (a) cho ta nghiệm ;
;
C2: lấy điều kiện khi
khi 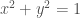 cho ta nghiệm
cho ta nghiệm  .
.
Chú ý rằng các điều kiện đưa thêm phải tương thích với điều kiện đã cho, cụ thể tại giao điểm của đường tròn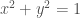 và trục hoành
và trục hoành 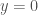 giá trị của nghiệm từ hai điều kiện đã cho và thêm vào phải giống nhau!
giá trị của nghiệm từ hai điều kiện đã cho và thêm vào phải giống nhau!
Một cách khác lấy điều kiện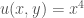 khi
khi 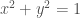 ta có nghiệm
ta có nghiệm
Cũng cần lưu ý với sẽ không có nghiệm nào thỏa mãn câu c! Tại sao?
sẽ không có nghiệm nào thỏa mãn câu c! Tại sao?
Lý do xảy ra hiện tượng vô số nghiệm trong câu c là vì:
– Jacobian tại các điểm trên đường cong ban đầu bị triệt tiêu, nghĩa là
bị triệt tiêu, nghĩa là
trong đó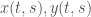 là hình chiếu xuống mặt phẳng Oxy của đường đặc trưng có thời điểm ban đầu
là hình chiếu xuống mặt phẳng Oxy của đường đặc trưng có thời điểm ban đầu
– hơn nữa, đường cong ban đầu chính là một đường đặc trưng.
Tôi đã chấm xong bài tập cho lớp K57TN. Một vài nhận xét:
– Nhóm 3: làm bài khá ẩu, rất nhiều bài nhóm không chỉ rõ là bài tập nào, ở đâu. Những bài như vậy tôi không chấm.
– Một số bài khi điều kiện Jacobian không thỏa mãn các bạn đã biết cách tìm thêm các nghiệm bằng cách cho thêm điều kiện.
– Rất nhiều lỗi sai giống nhau! Chẳng hạn việc tính giới hạn
các bài đều cho cùng giới hạn 1. Điều này chỉ đúng khi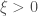 .
.
Thưa thầy hôm nay đã là 27 Tết,em biết thầy rất bận ko có thời gian trả lời chúng em được. Nhưng em mạn phép xin thầy giảng cho em bài 7/Exercises 3.4 (trang 133,sách Asmar) với ạ. Em tìm được khai triển của g* rồi nhưng đến đoạn tìm nguyên hàm G và tìm nghiệm thì ta chia trường hợp như thế nào ạ?
Tôi vừa chấm bài đó. Bài làm như đã nộp chưa thác triển tuần hoàn chu kỳ 2. Hàm thác triển
Để ý rằng
nên nguyên hàm
là hàm tuần hoàn chu kỳ 2.
Khi đó
và G(x+2)=G(x). Viết gọn lại
G(x)=10|x-2n| khi 2n-1<x<2n+1.
Nghiệm cho bởi công thức D’Alembert
Không dễ để viết tường minh nhưng ta có thể vẽ đồ thị nghiệm tại một số thời điểm. Ngoài ra ta có thể thấy nghiệm sẽ không có đạo hàm riêng theo x tại các điểm (x, t) chỉ thuộc vào một đường đặc trưng
x-t=n hay x+t=n với n là số nguyên.
Thầy ơi,em vẫn chưa hiểu đoạn khai triển tuần hoàn chu kì 2 thì phải là (-1)^(n+1) chứ ạ?
Với lại tích phân của hàm g*(x)dx từ n đến n+2 tại sao lại bằng 0 ạ? Em thấy nó luôn dương mà thầy.
Em đúng rồi, tôi nhầm. Còn tích phân, em lấy n=-1 chẳng hạn.
Dạ em vẫn chưa hiểu bài làm của thầy lắm ạ. Lấy n=-1 hay là bằng bao nhiêu nữa thì tích phân vẫn luôn nhận giá trị dương ạ.
Tích phân từ n đến n+2, hàm g^* luôn có một nửa chìm dưới trục hoành và nửa còn lại nổi lên trên trục hoành.
Vâng ạ,em không để ý kĩ. Thầy cho em hỏi nốt chỗ G(x)=10|x| khi -1<x<1 ?
Sửa lại
G(x)=-10|x| khi -1<x<1.
Chỗ này dùng công thức
Xét từng trường hợp 0<x<1 và -1<x<0.
Vâng ạ,em cảm ơn thầy. Em chúc thầy và gia đình năm mới sức khỏe,hạnh phúc.
Tôi đã chấm xong bài tập cho lớp K57A1T. Một vài nhận xét như sau.
– Nhóm 3 làm bài không tốt. Mắc lỗi giống nhóm 3 lớp K57TN, không ghi rõ bài tập ở đâu. Một số lỗi đơn giản như khi chuyển về dạng chính tắc, đến bước thay vào phương trình quên một vài số hạng trong phương trình ban đầu.
– Nhóm 5 không biết phân loại phương trình, chẳng hạn bài 1 trong đề giữa kỳ K52A2 nhóm 1 yêu cầu xác định loại phương trình
Nhóm tính
và kết luận phương trình đã cho là hyperbolic. Điều này là sai, cần chú ý .
.
– Một số bài khi lấy nguyên hàm còn thiếu hằng số.
Điểm cần lưu ý nữa: khi giải bài toán biên hỗn hợp của phương trình truyền sóng có điều kiện biên không thuần nhất thì chưa thể dùng công thức D’Alembert dạng thác triển. Muốn dùng công thức D’Alembert dạng thác triển cần phải khử điều kiện biên.
Thưa thầy , thầy có thể gợi ý em cách làm bài 4.17 , trang 96 sách của Pinchover được không ạ .
Câu a, b có cách giải giống nhau qua các bước sau.
B1: Em chuyển về dạng chính tắc.
B2: Tìm nghiệm tổng quát.
B3: Áp nghiệm tổng quát vào các điều kiện ban đầu để tìm nghiệm của bài toán.
Câu c khá dễ.
Câu d kiểm tra các hàm u, v, w có chẵn, lẻ, tuần hoàn, theo biến x hay không?
Câu e tính toán đơn thuần.
Thưa thầy , như vậy ở câu a phải hiểu yêu cầu ” Không sử dụng công thức D’Alembert ” là em không được viết trực tiếp công thức nghiệm luôn ( đầu trang 89 ) mà cần phải làm rõ từng bước như thầy hướng dẫn ở trên ạ .
Khác với cách đưa ra công thức D’Alembert tôi dạy trên lớp, sách của Pinchover-Rubinstein sử dụng công thức Green (mối liên hệ giữa tích phân bội hai lớp và tích phân đường) để dẫn ra công thức D’Alembert. Yêu cầu “không sử dụng công thức D’Alembert” ở trang 89 trong sách của Pinchover-Rubinstein cần hiểu theo ý này. Về thực chất ba bước tôi đưa ra cũng chỉ là một cách khác sách của Pinchover-Rubinstein để đi tới công thức D’Alembert. Cũng có thể còn có cách thứ ba khác để dẫn tới công thức này?
Bài tập phần truyền sóng-truyền nhiệt cho lớp K57A1T
Tôi có sử dụng thêm cuốn
“PDEs – BVPs with applications” của M.A. Pinsky.
Đường link
http://gen.lib.rus.ec/book/index.php?md5=99D8FD67729A89A12F4EBC89BE5A4771
Bài tập lần 2 cho lớp K57TN
https://www.dropbox.com/s/vygv9nkdgjx5gfl/BTPTDHR_K57TN.rar?dl=0
Thưa thầy , thầy có thể dán đường link tải cuốn sách của Gunther lên được không ạ . Em cảm ơn .
Cuốn đó tôi không có bản điện tử.
Em thưa thầy , thầy có thể giải thích cho em hàm G ở trong công thức nghiệm của bài 4 trang 176 sách của Guenther không ạ . Em cảm ơn .
Hàm G này là hàm Green cho bài toán hỗn hợp cho phương trình truyền nhiệt trên nửa trục với điều kiện biên Dirichlet thuần nhất, cụ thể
Dùng thác triển lẻ ta chuyển được bài toán trên thành bài toán trên toàn đường thẳng. Từ hàm Green trên toàn đường thẳng ta có thể tính được hàm Green trên nửa trục.
Chú ý công thức nghiệm cho bài toán trên nửa trục
với là hệ số khuếch tán,
là hệ số khuếch tán, 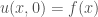 là điều kiện ban đầu.
là điều kiện ban đầu.
Một cách tương tự với hàm Neumann N ở bài 8/trang 177 trong sách của Guenther-Lee. Khác một chút so với bài 4/trang 176 bạn Tiến Tài hỏi ở trên là điều kiện biên là điều kiện Neumann thuần nhất nên ta thác triển chẵn. Khi đó hàm N được tính qua hàm Green k trên toàn trục như công thức được cho trong bài 7/trang 177.
em thưa thầy, thầy giúp em đề bài (b) 11 trong sách Asmar với ạ.
Em có thể nói cụ thể bài 11 trang bao nhiêu không?
em thưa thầy bài 11 trang 152 sách Asmar ạ
Từ bài 11-14/trang 152, sách của N. K. Asmar, yêu cầu giải bài toán như Example 3/trang 150 với điều kiện ban đầu được cho trong từng bài. Bài toán trong Example 3/trang 150 được giải một cách tổng quát trong Example 2/trang 147 với các hằng số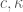 và chiều dài cụ thể.
và chiều dài cụ thể.
Thưa thầy!thầy gợi ý giúp em bài 73/tr434 sách thầy Hợp vs ak?với lại em hỏi thế nào là nghiệm không giới nội ak?em cảm ơn thầy!
Bài này ta mò một nghiệm dạng tách biến tổng:
u(x, t)=X(x)+T(t).
Nghiệm không giới nội là nghiệm không bị chặn, nghĩa là có một dãy điểm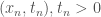 sao cho
sao cho
Hình ảnh các đường đặc trưng cho bài 15/trang 34 trong giáo trình của GS. Bernard
và bài 10/trang 31
thầy dịch và hướng dẫn cho nhóm e bài 17,19trang 150-152 trong sacha của M.A.Pinsky với ạ.e cảm ơn ạ!
Em làm như hướng dẫn trong bài tập, cụ thể:
– chuyển từ phương trình ban đầu sang phương trình truyền sóng bằng cách đặt như bài 17,
– với bài còn lại, dùng cách đặt ở bài 17 chuyển các điều kiện ban đầu ta thu được bài toán giá trị ban đầu cho phương trình truyền sóng trên toàn đường thẳng, từ đó dùng công thức D’Alembert để giải bài toán sau khi đặt,
– chú ý chuyển ngược lại nghiệm y tìm được trên về nghiệm u.
Thưa thầy, thầy hướng dẫn cho em bài 12-13 trang 109 sách M.A.Pinsky với ạ..
Em cảm ơn thầy
Bài 12 em thay nghiệm dạng tách biến phức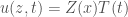 vào phương trình truyền nhiệt sẽ tìm được nghiệm như yêu cầu. Chú ý
vào phương trình truyền nhiệt sẽ tìm được nghiệm như yêu cầu. Chú ý
– nghiệm bị chặn, đặc biệt khi quan sát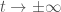 , nên các hằng số (giá trị riêng hay còn gọi là phổ) là các số phức dạng
, nên các hằng số (giá trị riêng hay còn gọi là phổ) là các số phức dạng 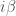 ,
,
– khi đó sẽ tính được qua
qua  với chú ý số ảo
với chú ý số ảo  có hai căn bậc hai
có hai căn bậc hai  .
.
Bài 13 yêu cầu tách phần ảo, phần thực của các nghiệm bài 12 sẽ được các dạng nghiệm trong bài 13.
Bài 14 yêu cầu lấy tổ hợp tuyến tính các nghiệm trong bài 13 phù hợp với điều kiện biên ở trên và nghiệm dừng để giải bài toán ở trên.
Nếu không có gì thay đổi sáng thứ Tư, ngày 08/04/2015, các bạn lớp K57A1T và K57TN sẽ thi giữa kỳ môn PTĐHR. Lớp K57A1T sẽ tách thành hai nhóm, một nhóm thi tiết 1, nhóm kia thi tiết 2. Lớp K57TN làm bài trong thời gian hai tiết. Các bạn được sử dụng mọi tài liệu, trừ tài liệu của sinh viên khác. Nội dung thi các kiến thức trong bài tập về nhà hai lần vừa rồi.
thưa thầy!e hỏi bài 4.14/96 sách của pinchover có sử dụng đặt w=u-v
với v(x,t) là 1 nghiệm riêng của pt sóng không thuần nhất,vậy e hỏi v(x,t) tìm như nào thế ak?vs lại e hỏi ta có thể sử dụng trực tiếp công thức Dalambert vào bài này đc ko ak?
Bài này dùng công thức D’Alembert cho phương trình không thuần nhất. Trong công thức có chứa tích phân bội trên nón phụ thuộc. Chi tiết em xem công thức (4.17) trang 89.
Ngoài ra em có thể tham khảo thêm bài
https://bomongiaitich.wordpress.com/2012/04/10/cong-th%E1%BB%A9c-dalembert-cho-ph%C6%B0%C6%A1ng-trinh-hyperbolic-khong-thu%E1%BA%A7n-nh%E1%BA%A5t/
Thưa thầy ,đề bài của bài 5.15 trong sách của Pinchover là gì đấy ạ.Thầy hướng dẫn em bài 5.6 trong sách của Pinchover với ạ .Em cảm ơn thầy!
Bài 5.15 yêu cầu chứng minh tính duy nhất nghiệm của bài toán bằng cách xây dựng tích phân năng lượng phù hợp.
Bài 5.6 yêu cầu dùng tách biến tìm nghiệm của bài toán. Em tìm các nghiệm tách biến không tầm thường của phương trình và các điều kiện rồi lập chuỗi nghiệm. Cuối cùng dùng điều kiện ban đầu tính hệ số. Tiếp đến tính giới hạn khi t ra vô cùng và chứng minh tính tuần hoàn theo x của nghiệm.
thưa thầy, thầy hướng dẫn em bài 3(trang 150) và bài 20(trang 108-109) sách Mnsky với ạ.
Bài 20/trang 109 yêu cầu tìm nghiệm dừng (steady state) của bài toán. Chú ý rằng nghiệm dừng không phụ thuộc vào thời gian nên
của bài toán. Chú ý rằng nghiệm dừng không phụ thuộc vào thời gian nên  . Như vậy hàm
. Như vậy hàm 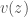 là hàm một biến và thỏa mãn phương trình cấp 2 với hai điều kiện biên. Từ đó em tính ra được nghiệm dừng.
là hàm một biến và thỏa mãn phương trình cấp 2 với hai điều kiện biên. Từ đó em tính ra được nghiệm dừng.
Bài 3/trang 150 hỏi từ giả thiết đã cho dẫn đến điều gì với các hệ số B_n. Em thay s=L/3 vào công thức chuỗi rồi đồng nhất hệ số. Chú ý giá trị của khi số tự nhiên
khi số tự nhiên 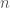 thay đổi.
thay đổi.
việc kiểm tra 1 ngiệm có phải là nghiệm cổ điển không thì ta xét nó có tồn tại đạo hàm trên toàn miền đang xét phải không ạ. Nghiệm dừng của bài toán là gì ạ. Với cả khi bài toán nói là hai đầu dây cố định là bài toán Dirichlet, nếu một đầu cố định tại o :u(0,t)=…, đầu tại L tự do u’x(L,t)=….., hai đầu tự do là bài toán newman ạ?
Em viết đúng rồi. Chỉ bổ sung thêm
– hai đầu cố định là có điều kiện biên Dirichlet thuần nhất,
– hai đầu tự do là có điều kiện biên Neumann thuần nhất,
– với nghiệm cổ điển ngoài việc có đạo hàm riêng trên toàn miền, các đạo hàm riêng cần thỏa mãn phương trình đã cho + thỏa mãn các điều kiện biên hay ban đầu.
Thầy có thể hướng dẫn chi tiết em làm bài 5.15 trong sách của Pinchover được không ạ.Em cảm ơn!
Để chứng minh tính duy nhất nghiệm ta giả sử nó có hai nghiệm u_1, u_2, rồi chứng minh u_1=u_2 hay hiệu v=u_1-u_2=0. Chú ý u_1, u_2 là hai nghiệm của cùng bài toán nên v là nghiệm của bài toán thuần nhất, giống như tôi trình bày với các bài toán truyền sóng, truyền nhiệt. Sau đó xét tích phân năng lượng
Chứng minh với mọi
với mọi 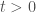 bằng cách
bằng cách
+ tính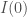 ,
,
+ tính đạo hàm
với chú ý v là nghiệm của bài toán thuần nhất.
Sử dụng dẫn đến v có các đạo hàm riêng bằng 0. Từ đó v=const. Lại từ điều kiện ban đầu thuần nhất dẫn đến v=0. Đây chính là điều cần chứng minh.
dẫn đến v có các đạo hàm riêng bằng 0. Từ đó v=const. Lại từ điều kiện ban đầu thuần nhất dẫn đến v=0. Đây chính là điều cần chứng minh.
Thưa thầy, thầy giảng giúp em bài 6 trang 108 sách M.A.Pinsky với ạ..Em cảm ơm thầy
Bài 6/trang 108 giống bài 20/ trang 109, cùng yều cầu tìm nghiệm dừng. Cụ thể bài 6/trang 108 yêu cầu tìm nghiệm dừng u(x, y, z, t)=v(z) chỉ phụ thuộc vào z. Khi đó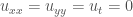 . Chú ý
. Chú ý 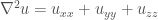 . Từ đó ta có phương trình cấp 2 với hai điều kiện biên cho hàm một biến v(z). Sau khi tính được v(z), đề bài yêu cầu tính dòng nhiệt đi qua đầu z=L nghĩa là tính
. Từ đó ta có phương trình cấp 2 với hai điều kiện biên cho hàm một biến v(z). Sau khi tính được v(z), đề bài yêu cầu tính dòng nhiệt đi qua đầu z=L nghĩa là tính 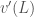 .
.
16/03/2015 có bạn hỏi tôi về phương trình dao động của thanh rầm (beam)
Nó có thể có các điều kiện biên như sau:
– điều kiện kẹp chặt ở đầu trái (the beam is clamped at the left)
– điều kiện simply supported ở đầu trái
– điều kiện tự do (free) ở đầu trái
Chi tiết các bạn có thể tham khảo
http://en.wikipedia.org/wiki/Beam_(structure)
Để chứng minh tính duy nhất ta xét tích phân năng lượng
Sau đó
+) tính ,
,
+) tính .
.
Một câu hỏi khác về điều kiện biên của phương trình truyền nhiệt
từ đâu ra?
Nó từ “Newton’s law of cooling” nói rằng dòng nhiệt truyền ra tại đầu x=0 tỷ lệ thuận với độ chênh lệch nhiệt độ giữa đầu x=0 và môi trường, chẳng hạn ở đây nhiệt độ ngoài môi trường bằng 0.
Chú ý: dòng nhiệt thoát ra ngoài môi trường
– tại x=0: ,
,
– tại x=L: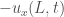 .
.
Thưa thầy , thầy có thể giải đáp giúp em :
– Bài 3,6 file pdf của Bernard , yêu cầu tuyến tính hóa xung quanh lời giải 0 ở đây là em sẽ phải làm gì ạ .
– Cũng bài 3 trên ở câu b , yêu cầu là tìm ” dispersion relation ” .Tuy nhiên đây là bài toán 3 biến x,z,t thì định nghĩa ” dispersion relation ” là như thế nào ạ .
– Thầy có thể chụp bài 4 , chương 1-3 sách của Guenther để em biết ” Newton’s law of cooling ” ( bài tập 5 trang 153 yêu cầu sử dụng ) .
Bài 4/ 1.3
Bài 3, 6/ Bernard yêu cầu tuyến tính hóa nghĩa là trong phương trình ta bỏ đi các phần phi tuyến.
Bài 3.b/ Bernard em cần tìm hai hàm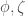 có dạng
có dạng
Khi đó
– dispersion relation :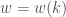 ?
?
Em thưa thầy, thầy hướng dẫn em làm bài 5 trang 133 sách M.A Pinsky với ạ!
E cảm ơn thầy!
Trước hết tìm nghiệm dừng v(z) thỏa mãn phương trình và điều kiện biên.
Đặt w(z, t)=u(z, t)-v(z). Khi đó w(z, t) thỏa mãn bài toán cho phương trình truyền nhiệt với điều kiện biên Neumann thuần nhất và điều kiện ban đầu mới. Dùng tách biến giải bài toán cho w(z, t).
Cuối cùng nghiệm u(z, t)=w(z, t)+v(z).
Hạn nộp bài tập lần 2 cho lớp K57A1T: sáng thứ Sáu, ngày 20/03/2015. Tôi có mặt ở trường từ 9h00 tại phòng 409T3. Có gì các bạn gọi cho tôi qua số 0936 585 511.
Về danh sách thi giữa kỳ của lớp K57A1T:
Nhóm 1: thi từ 7h00 đến 7h50
1. Nguyễn Thị Mai Anh
2. Nguyễn Thị Ngọc Ánh
3. Nguyễn Thị Diệp
4. Nguyễn Phương Dung
5. Nguyễn Thị Thu Hà
6. Tô Thị Thu Hằng
7. Trần Thị Hằng
8. Đỗ Thị Hiên
9. Nguyễn Thị Hiền
10. Nguyễn Thị Thu Hòa
11. Ngô Thị Huyền
12. Nguyễn Đức Hưng
13. Nguyễn Thị Hương
14. Phạm Thị Diệu Hương
15. Phan Đình Kiên
16. Kiều Thị lan
17. Lê Thị Lan
18. Phạm Ngọc Linh
19. Trần Thị Linh
20. Nguyễn Thị Lương
21. Tô Thị Ngọc Mai
Nhóm 2: thi từ 8h00 đến 8h50
1. Nguyễn Thị Mơ
2. Đỗ Thu Ngà
3. Lưu Hồng Minh Ngọc
4. Phùng Thị Minh Nguyệt
5. Ngô Thị Nhã
6. Nguyễn Thị Thanh Nhàn
7. Nguyễn An Ninh
8. Mai Thanh Quang
9. Bùi Thị Quỳnh
10. Nguyễn Thu Quỳnh
11. Trần Thị Như Quỳnh
12. Dương Minh Tân
13. Phạm Thị Thắm
14. Trần Thị Thới
15. Nguyễn Lệ Thủy
16. Trần Thị Hoài Thương
17. Nguyễn Thị Hồng Trang
18. Dương Thị Vân
19. Trần Xuân Vinh
20. Nguyễn Văn Vũ
Các bạn nhớ mang theo thẻ sinh viên, nếu không có sẽ không được thi.
Thưa thầy,thầy hướng dẫn em bài 20 trang 152 sách Pinsky với ạ.
Em tìm nghiệm dạng
thưa thầy sử dụng đk biên để tìm nghiệm đúng ko ạ?
khi nghiệm thỏa mãn pt đã cho thì e hơi bị rối ạ?
Phương trình cho A(s), B(s) em tìm được là như nào? Từ điều kiện biên dẫn đến điều kiện cho A, B?
em thưa thầy. trong nghiệm tách biến có chứa Ao thì Ao tìm theo công thức nào ạ?
Chuỗi nghiệm của em như nào?
Thầy ơi thầy gợi ý giúp em bài Giữa kì lớp K55A3 -N1-B2 ạ.
Bài toán bạn lập được là gì?
Utt(x,t)=Uxx(x,t) – Ut(x,t)
với ĐK biên: U(0,t)=U(Pi,t)=0
và ĐK ban đầu: Ut(x,0)=0, U(x,0)=(sinx)^3.
Bài này dùng tách biến làm như bình thường đúng không ạ? Nếu vậy thì em biết làm rồi ạ.
Đúng vậy. Chú ý khi tìm nghiệm tách biến U(x, t)=X(x)T(t) ta gặp phương trình đối với T(t) như sau
Khi đó sẽ có hiện tượng tắt dần.
Thưa thầy, thầy viết cho em công thức nghiệm của phương trình dạng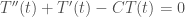 với.
với.
Có biệt số
TH1: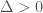 , nghiệm tổng quát của PT em cho
, nghiệm tổng quát của PT em cho
TH2: , nghiệm tổng quát của PT em cho
, nghiệm tổng quát của PT em cho
TH3: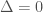 , nghiệm tổng quát PT em cho
, nghiệm tổng quát PT em cho
thưa thầy , thầy gợi ý rõ hơn cho em đề giữa kì k56MAT1 -Đ 4 -B2
Bài này dùng sóng tiến, sóng lùi. Chi tiết những bài như này tôi đã chữa vài lần trên lớp. Em thử viết công thức cụ thể của sóng tiến, sóng lùi và vẽ đồ thị?
Thưa thầy, bài này nếu viết sóng tiến sóng lùi thì em chỉ viết được hàm F(x) mà khi thác triển chẵn thì hàm f(x)= cos 3x với x tiến ra tới vô cùng.. Như vậy em không biết cách tìm nghiệm bị chặn bằng cách nào ạ.
Hình như em hỏi bài không nằm trong bài tập tôi giao. K56MAT1-D4-B2 tôi có giải thích phía dưới là đề giữa kỳ lớp MAT2024-1 (lớp K56 toán tin) đề 4 bài 2, còn bài em hỏi là đề giữa kỳ lớp MAT2010 (lớp K56A1T) đề 4 bài 2. Với bài em hỏi thác triển chẵn rồi dùng công thức nghiệm Poisson dạng tích phân rồi tính tích phân sẽ được nghiệm. Em có thể tham khảo đáp án bài tương tự, bài 2 trong đề cuối kỳ lớp K56A1T.
20/03/2015 tôi đã nhận bài tập của sáu nhóm, riêng nhóm 7 chưa nộp.
Trong thời gian chờ nhóm 7, tôi xem qua bài tập nhóm thấy có nhiều bài các bạn không ghi rõ nó nằm ở đâu, chẳng hạn sách nào và trang bao nhiêu. Những bài như vậy tôi sẽ không chấm điểm.
Ngoài ra, bài tập K56MAT1-D4_B2 như bạn Ngọc hỏi trên không thuộc vào danh sách bài tập tôi giao. Nhóm 5 có bài K56MAT1-D1-B1 cũng có tình trạng nhầm thành bài K56A1-D1_B1. Các bài này nằm trong đề thi giữa kỳ của K56 toán tin chứ không phải của lớp K56A1T. Lý do có lẽ các bạn không đọc phần Ghi chú phía dưới
K56MAT2-D4-B3: đề thi giữa kỳ lớp MAT2024-2 khóa K56, đề 4, bài 3,
chú ý
K56A1 là lớp MAT2010.
Việc các bạn nhầm bài K56MAT… có vẻ như xảy ra ở cả sáu nhóm. Để có công thức chuỗi nghiệm nếu các bạn không diễn giải sẽ bị trừ điểm.
Nhóm 1: làm sai đề rất nhiều chẳng hạn bài GK-K53A3_N3_B3 yêu cầu giải bài toán cho phương trình truyền sóng lại làm bài về truyền nhiệt; bài 1/tr 162, bài 8/tr 162 trong sách N. H. Asmar, đều nhầm tốc độ lan truyền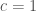 , trong khi đề ra
, trong khi đề ra  ; một số bài không nói rõ nằm trong sách nào, một số bài khác lại không nói nằm ở trang nào. Điểm nhóm này ở dưới mức TB.
; một số bài không nói rõ nằm trong sách nào, một số bài khác lại không nói nằm ở trang nào. Điểm nhóm này ở dưới mức TB.
Nhóm 2: cũng giống nhóm 1 bài 2/tr 162, hay bài GK-K54A2-D4-B2 cho tốc độ lan truyền 5 khi giải lại lấy bằng 3, đề cho hai đầu tự do khi giải lại cho hai đầu cố định. Điểm nhóm này ở mức TB.
Nhóm 3: cũng có một số bài không nói rõ ở trang nào. Điểm nhóm này ở mức TB khá.
Nhóm 4: cũng có bài không nói rõ trang nào. Điểm nhóm này dưới TB.
Nhóm 5: có rất nhiều bài không rõ số trang. Điểm dưới TB.
Nhóm 6: có rất nhiều bài không rõ trong sách nào. Các bạn trong nhóm này hình như chỉ làm bài cho mình chứ không muốn cho người khác, cụ thể người chấm bài, biết mình làm bài gì, có nằm trong những bài được giao hay không?
Em chào thầy. Thầy có thể giải thích cho em bài 9 câu a trang 153 của sách của Guenther được không ạ?
9. a) Interpret the boundary value problem
$u_t=a.u_{xx}, 0<x0,$
$u(x,0)=f(x), 0 \le x \le L,$
$u_x(0,t)- \mu u(0,t)=0, u_x(L,t)+\mu u(L,t)=0,t \ge 0,$
where $\mu >0$ is a constant, as a heat conduction model. What does the condition at $x=0$ mean? Why should the sign be a minus at $x=0$ and a plus at $x=L$?
Tạm dịch: Bài toán biên “…” là mô hình quá trình truyền nhiệt. Các điều kiện tại x=0 nghĩa là gì? Tại sao dấu tại x=0 là dấu trừ còn tại x=L lại là dấu cộng.
Ý nghĩa tại x=0: có sự truyền nhiệt tại đầu x=0. Dấu + hay trừ do “Newton’s cooling law”. Tôi đã chụp ảnh cái này trong phần trả lời bạn Nguyễn Tiến tài ở phía trên. Em đọc nhé.
Trong bài 6 trang 165 sách của Guenther có nói mục (3-22), thầy có thể chụp lại được không ạ?
Đó là công thức (3-22). Tôi chụp cách xây dựng công thức này, em lấy ở đây nhé
https://www.dropbox.com/s/zp4enr3synacexq/Green.rar?dl=0
Thưa thầy , trong những bài sử dụng phương pháp tách biến , sau khi đưa về giải phương trình vi phân chẳng hạn X”’ + aX = 0 nhưng dựa vào điều kiện ban đầu ta chỉ xây dựng được phương trình ẩn a ( ví dụ tan(a) = a/2) mà không thể giải đúng được a thì sẽ xây dựng công thức nghiệm như thế nào được ạ .
Ví dụ bài 8 , trang 217 sách của Gunther
Khi tìm nghiệm tách biến không dùng điều kiện ban đầu, initial condition, chỉ sử dụng phương trình và các điều kiện biên, boundary conditions. Bài 8/tr 217 trong sách Gunther-Lee tôi dẫn ra phương trình kiểu
Có thể thấy phương trình này có vô số nghiệm âm, trong từng chu kỳ của hàm cosine nó có đúng một nghiệm. Nên vẽ đồ thị để thấy điều này. Ký hiệu dãy nghiệm ta sẽ thu được dãy phổ. Lập công thức chuỗi nghiệm hình thức rồi dùng điều kiện ban đầu tính hệ số chuỗi nghiệm.
Tôi không hiểu em dẫn đến phương trình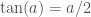 từ bài nào?
từ bài nào?
em thưa thầy gợi ý giúp em bài 1 trang 205, sách của grunther lee!
sau khi tách biến có X””/X =c , nếu c=0 thì X=ax^3+bx^2+cx+d, với điều kiện lim u(x,0)->0 khi x ra vô cùng, thì có suy ra luôn là a,b,c,d=0 không ạ
Bài này nên dùng biến đổi tích phân Fourier theo biến x. Em đọc bài “Sử dụng tích phân Fourier để giải PTĐHR”. Sáng nay tôi có nói dùng tách biến, cách tiếp cận này không tốt.
Tôi đã chấm xong bài tập nhóm cho lớp K57TN. Một lỗi hay gặp
Nhóm 1 và 3 có nhiều lỗi sai giống nhau khi làm các bài tập của GS. Bernard.
Nhóm 2 làm tốt hơn cả. Tuy nhiên bài 6.12 trong sách của Pinchover-Rubinstein đã được sửa lại trong bản các lỗi, nhưng nhóm không để ý.
Sáng nay tôi bị mắc bài dùng hàm Neumann (hàm Green cho bài toán biên với điều kiện biên Neumann) để giải bài toán với điều kiện biên không thuần nhất:
Hàm Neumann của bài toán có dạng
Với bài toán có điều kiện biên Dirichlet
có lời giải
trong đó hàm Green
Với bài toán biên Dirchlet trên nửa trục
ta có công thức nghiệm
với hàm Green
trong đó nghiệm cơ bản của phương trình truyền nhiệt trên toàn đường thẳng
trên toàn đường thẳng
Còn với bài toán biên có điều kiện Neumann trên nửa trục
ta có công thức nghiệm
với hàm Neumann
Tôi nghĩ nghiệm của bài toán biên Neumann trên một đoạn mà tôi còn mắc ở trên có dạng
Chú ý từ công thức tổng Poisson ta có mối liên hệ giữa hàm Green trên đoạn hữu hạn và trên nửa trục, cũng như hàm Neumann như sau:
Các bạn có thể tham khảo
Click to access lpde102.pdf
Một trong các vấn đề chính của các công thức nằm ở việc chứng minh hàm
là nghiệm của bài toán
Chú ý nên
nên
Khi đó
chứ không phải
Điểm quan trọng nữa trong các công thức
chứ không phải
Nói cách khác giá trị ban đầu và giá trị biên của các nghiệm là một quá trình lấy giới hạn.
Thưa thầy bài 2 đề 2 của đề giữa kì của lớp K57A1C có cho dữ kiện 2 đầu tự do. Vậy 2 đầu tự do thì U(0,t) và U(1,t) ở đây bằng gì ạ?
Em xem trong file
Click to access y_nghia_dk_ptdhr1.pdf
Bài tập PTĐHR lần 3 cho lớp K57TN
https://www.dropbox.com/s/t1owsiw5t9fjjfo/BT_L3_K57TN.rar?dl=0
Tôi có lấy một số bài tập trong cuốn
“Applied Partial Differential Equations with Fourier Series and
Boundary Value Problems, Fourth Edition ” của R. Haberman.
http://gen.lib.rus.ec/book/index.php?md5=af9a5124661d723ad09026ac0387ad4c
Bài tập của GS. Bernard cả ba nhóm đều phải làm hết.
Bài tập phần phương trình Laplace cho lớp K57A1T
Tôi có lấy một số bài tập từ cuốn
“BVPs and PDEs” của D. L. Powers.
Đường link
http://gen.lib.rus.ec/book/index.php?md5=14659491643EB21E2042FE81B73CA28B
em thưa thầy, thầy giúp em hình vẽ của g*(x) trong bài k57a1cđ1b2 với ạ
đề giữa kỳ thầy ạ
Có phải em hỏi bài giữa kỳ? Em có thể viết công thức của g*?
dạ vâng đề giữa kỳ thầy ạ. em cũng vẽ hình để viết ra công thức nhưng mà em không thể viết được công thức , có lẽ hình của em vẽ sai, em muốn hỏi thầy hình của g*(x) ạ
Công thức thác triển chẵn
Em thử dùng công thức này để viết g*?
thưa thầy e hỏi ak!với phương trình chính tắc dạng là 25v_nn-10v_n=15e^n thì ta tìm dạng tổng quát thế nào ak?
C1. Tìm một nghiệm riêng: vế phải có dạng đặc biệt nên ta tìm nghiệm riêng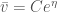 . Thay vào phương trình sẽ tìm được C. Sau khi tìm được C nghiệm tổng quát
. Thay vào phương trình sẽ tìm được C. Sau khi tìm được C nghiệm tổng quát
trong đó là nghiệm tổng quát của phương trình
là nghiệm tổng quát của phương trình
C2. Viết lại
Sau đó tích phân dần lên.
thưa thầy!thầy có thể cho e biết kết quả đc ko ak?
Em viết kết quả em tính được?
e chưa tính ra được thầy ak!e đag làm cách 2,bình thường một vế bằng 0 thì ta suy ra đc luôn nhưng trong câu này e ko biết làm thế nào nữa ak
Em tích phân như trường hợp bằng 0. Không biết em có đi học đầy đủ? Những kỹ năng này tôi đều nói trên lớp.
vaag.e cam ơn thầy
15/04/2015 tôi trình bày phần nguyên lý cực đại:
– cho hàm điều hòa trong miền bị chặn,
– cho hàm điều hòa ngoài hình tròn,
– cho nghiệm của phương trình truyền nhiệt.
Trong trường hợp phương trình truyền nhiệt tôi vẫn mắc vài điểm. Các bạn có thể xem trong sách thầy Hợp hoặc tham khảo
https://bomongiaitich.wordpress.com/2012/08/18/nguyen-ly-cuc-dai-tiep/
Thầy hướng dẫn cho em bài 7.13 trong sách pinchover trang 204-207 với ạ.Em cảm ơn!
Đây là bất đẳng thức Harnack, tôi đã dạy trên lớp. Em sử dụng công thức Poisson.
thưa thầy!trong bài 7.15-sách Pinchover,câu a có nói đến cực đại đia phương,thầy có thể giải thích giúp e được không ak?
Hàm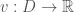 được gọi là có cực đại địa phương nếu
được gọi là có cực đại địa phương nếu
có một điểm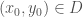 và số dương
và số dương  sao cho
sao cho
với bất kỳ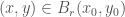 (hình tròn tâm
(hình tròn tâm 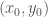 bán kính
bán kính  đủ nhỏ để nó nằm trong
đủ nhỏ để nó nằm trong  ) ta có
) ta có
Thưa thầy..thầy dịch và hướng dẫn cho em bài 7.7 và 7.14 trang 204-207 sách Y.Pinchover với ạ.
Em cám ơn thầy
Bài 7.7: (a) yêu cầu viết phương trình Laplace trong hệ tọa độ cực; (b) yêu cầu giải bài toán biên Dirichlet cho phương trình Laplace (hàm điều hòa là nghiệm của phương trình Laplace) trong hình tròn với điều kiện biên trên đường tròn
với điều kiện biên trên đường tròn 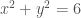 .
.
Để giải bài này em chỉ cần áp dụng công thức nghiệm trong hệ tọa độ cực rồi dùng điều kiện biên tính các hệ số. Nhớ quay trở lại biến (x, y).
Bài 7.14 quan tâm đến bài toán biên Neumann trong hình tròn. Câu (a) yêu cầu tìm các hệ số để bài toán vô nghiệm. Câu (b) yêu cầu giải bài toán với các hệ số khác câu (a).
Để giải bài này em chuyển sang hệ tọa độ cực. Điều kiện để bài toán có nghiệm là điều kiện tích phân trên đường tròn của điều kiện biên phải bằng 0. Khi có điều kiện này em sử dụng công thức nghiệm như bài 7.7. Chú ý pháp tuyến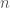 trong bài là pháp tuyến ngoài đơn vị nên khi thay điều kiện biên cần đạo hàm theo bán kính r chuỗi nghiệm.
trong bài là pháp tuyến ngoài đơn vị nên khi thay điều kiện biên cần đạo hàm theo bán kính r chuỗi nghiệm.
em thưa thầy, trong bài 7.7 trang 205 sách Y.Pinchover em không hiểu cho u(x,y)= y+y^2 để làm gì ạ?
Chú ý đề chỉ cho trên biên của đĩa
trên biên của đĩa  , nghĩa là lúc đó
, nghĩa là lúc đó 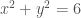 . Đây là điều kiện biên Dirichlet.
. Đây là điều kiện biên Dirichlet.
em thưa thầy, nghĩa là em tìm ra chuỗi nghiệm rồi thay vào u(x,y)=y+y^2 có phải không ạ
Đúng vậy, chú ý lúc đó x^2+y^2=6.
Thầy cho em đường link tải các đề thi cuối kỳ của các lớp khóa trước với ạ.Em cảm ơn thầy!
Em vào chuyên mục đề thi
https://bomongiaitich.wordpress.com/category/d%E1%BB%81-thi/
Thưa thầy,
Bài 9 trang 123 sách N.H.Asmar, hàm f(x)=x(1-x) ở ĐK ban đầu U(x,0)=f(x) không chẵn cũng không lẻ ạ.Như vậy có phải sai đề không ạ?
Điều kiện ban đầu chỉ xác định trong đoạn [0, 1] nên chưa liên quan gì đến tính chẵn lẻ. Do điều kiện biên là Dirichlet thuần nhất nên ta dùng kỹ thuật thác triển lẻ, tuần hoàn chu kỳ 2 lên toàn trục để sử dụng công thức D’Alembert. Việc thác triển này là bước trung gian và do ta tự nghĩ ra. Nếu không dùng cách thác triển này ta vẫn còn cách dùng phương pháp tách biến. Nói cách khác kết quả cuối cùng của bài toán này không liên quan gì đến tính chẵn lẻ của điều kiện ban đầu.
Em thưa thầy, thầy hướng dẫn e bài 6 trang 286 sách Power với ạ.
Em cảm ơn thầy!
Em tách thành hai bài toán con:
BT1: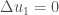
BT2: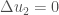
Nghiệm của bài toán ban đầu
thưa thầy e ko hiểu tại sao lại tách thành 2 btoan như thế ạ?
có thể là 2 bài toán sau đc ko?
BT1: : $\Delta u_1=0
u_1(0, y)=1, u_1(a, y)=0,
u_1(x, 0)=u_1(x, b)=1;$
BT2: $\Delta u_2=0
u_2(0, y)= u_2(a, y)=1,
u_2(x, 0)=1, u_2(x, b)=0$
à,em hiểu chỗ này rồi ạ!
Thưa thầy, thầy giúp em bài 18/275 Power với ạ!
Em sử dụng công thức nghiệm bài 16/tr 275.
Thưa thầy, thầy viết lại cho em hàm a), b) trong đề bài 8.1.4 trang 297 của sách của Gunther lee. Em cám ơn.
a)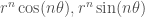 .
.
b) .
.
thầy giúp em xem lại đề 1c trang 269 sách power sao lại là u´x(x,0)=0 ạ. và thầy gợi ý cho em bài 11 trang 273 sách power với ạ?
Bài 1c/tr 269 đúng như em nhận xét, cần sửa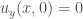 .
.
Bài 11/tr 273 em tìm các nghiệm tách biến (product solution) bị chặn như bài 10 yêu cầu, chú ý dùng thêm điều kiện u(0, y)=0. Sau đó lập công thức nghiệm dạng tích phân. Dùng điều kiện biên còn lại tính hệ số trong công thức nghiệm.
Trong một số bài các bạn gặp phải công thức nghiệm dạng tích phân. Để tính hệ số trong các công thức này các bạn tham khảo bài
https://bomongiaitich.wordpress.com/2013/04/10/tu-chuoi-fourier-den-tich-phan-fourier/
Chú ý: tích phân trên nửa trục hay toàn trục, tích phân dạng Fourier-sine hay Fourier-cosine.
Thưa thầy cho em hỏi tại sao ở Example 4 trang 131 sách H.N.Asmar lại có thể tính nghiệm tổng quát như vậy được mà không cần thác triển f và g ạ? Em cảm ơn thầy ạ.
Vì điểm (x, t) nằm trong miền I, trong hình 4 phía trên. Khi đó miền phụ thuộc của điểm nằm hoàn toàn trong [0, 1].
thưa thầy!ở bài 7.21/206 sách pinchover có yêu cầu sử dụng nguyên lí cực đại để chứng minh đẳng thức,thầy có thể hướng dẫn giúp em cách áp dụng nguyên lí cực đại như thế nào vào bài này đc không ak?
B1: chứng minh . Em xem giá trị
. Em xem giá trị  trên hai biên
trên hai biên 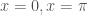 và trên
và trên 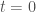 như nào rồi sử dụng nguyên lý cực đại.
như nào rồi sử dụng nguyên lý cực đại.
B2: chứng minh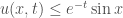 . Em hãy xét hàm
. Em hãy xét hàm 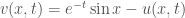 rồi xem hàm này thỏa mãn bài toán nào. Sau đó làm như B1.
rồi xem hàm này thỏa mãn bài toán nào. Sau đó làm như B1.
Thưa thầy,thầy dịch và hướng dẫn em làm bài tập 7.19 trang 206 sách Pinchover với ạ. Em cảm ơn thầy!
Đề bài cho hàm điều hoà trong hình tròn với giá trị trên đường tròn cho trước.
a) yêu cầu tính u(0, 0) mà không phải giải tường minh hàm điều hoà. Gợi ý dùng Định lý giá trị trung bình.
b) yêu cầu chứng minh các bất đẳng thức. Gợi ý quan sát bất đẳng thức trên đường tròn, sử dụng nguyên lý so sánh và nguyên lý cực đại mạnh.
Thầy hướng dẫn em bài 12 trang 287 sách D.L.Power với ạ
em thưa thầy, thầy giúp em đề bài 12 và 13 trang 287 sách Power với ạ
Trả lời cả bạn lan và vân:
các bạn thay f(x) vào công thức tích phân tính u(x, y) rồi tính tích phân đó.
Thưa thầy..thầy giúp em bài 34 trong sách thầy Nguyễn Thừa Hợp với ạ.
Em cảm ơn thầy
Bài 34 là bài toán biên Dirichlet trong vành khăn. Em chuyển về hệ tọa độ cực với chú ý điều kiện biên trên từng đường tròn ứng với từng bán kính để chuyển điều kiện biên sang hệ tọa độ cực. Em sử dụng công thức nghiệm dạng chuỗi rồi áp vào điều kiện biên. Đồng nhất hệ số từng điều kiện biên rồi ghép lại ta sẽ có hệ vô hạn các hệ đại số tuyến tính. Từ đó giải ra các hệ số. Cuối cùng thay vào chuỗi nghiệm và nhớ trả lại nghiệm dạng x, y.
thưa thầy, thầy hướng dẫn em giải bài 7.22 phần a, trang 207, sách pinchover với ạ! em chỉ chứng minh được <=, mà không biết bác bỏ được dấu = như thế nào, em cám ơn thầy ạ
Nếu u(x, y)-x=0 tại điểm nào đó trong D thì sử dụng nguyên lý cực đại mạnh sẽ dẫn đến điều vô lý. Em xem điều vô lý là gì?
Em làm được rồi ạ! em cảm ơn thầy!
Tôi đang chấm bài tập phần phương trình Laplace:
– nhóm 7: chỉ có hai bạn Nguyễn Văn Vũ và Dương Minh Tân làm bài,
– nhóm 7, 4, 2 làm được rất ít bài,
– một số nhóm viết khi chuyển sang hệ tọa độ cực là sai,
khi chuyển sang hệ tọa độ cực là sai,
– khi giải các bài toán trong hình tròn, ngoài hình tròn và trong vành các bạn chỉ cần sử dụng công thức nghiệm dạng chuỗi, một số bài thiết lập lại không đúng, chẳng hạn trong vành 1<r<2 không chứa gốc các bạn lại cho r=0?
– với bài toán biên Neumann các bạn chưa để ý hướng của pháp tuyến,
– nhóm 6 làm tốt hơn cả.
Thưa thầy , bài 18 trang 322 sách của Gunther-Lee có nói đến bất đẳng thức Schwarz trên hình cầu đóng . Thầy có thể cho em biết đó là bất đẳng thức nào được không ạ .
Đây chính là bất đẳng thức cơ bản Cauchy-Schwarz
http://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality
em thưa thầy nếu n là vecto pháp tuyến trong của hình tròn bán kính r thì
n = (-x/r,-y/r) ?
Đúng vậy. Pháp tuyến trong có gốc đặt trên biên, đường tròn, và hướng vào phía trong miền, trong hình tròn.
Thưa thầy , thầy có thể dịch yêu cầu bài 4 trong tờ đề của g.s Bernard được không ạ . Em cảm ơn .
Bài 4. Mối quan hệ toàn cục với k và (-k) cho phương trình truyền nhiệt trong đoạn hữu hạn được dùng để loại bớt hai trong bốn điều kiện biên. Tuy nhiên ở đó có vài hạn chế. Hãy kiểm tra xem điều gì xảy ra nếu bạn chỉ được cho hai điều kiện biên trên cùng một cạnh, và bạn cần xác định các điều kiện trên cạnh còn lại. Nói cách khác, điều gì xảy ra khi bạn thử giải h_0, h_1, từ hai quan hệ toàn cục, theo g_0, g_1? Để đơn giản bạn có thể giả sử các điều kiện trên cạnh x=0 bằng không, nghĩa là cả g_0 và g_1 đều bằng không.
Tôi đã vào điểm thường xuyên môn PTĐHR cho lớp K57A1T+K57TN. Nếu các bạn cần có thể gặp tôi sáng mai 14/05/2015.
Bọn e có thể gặp thầy ở đâu để xem điểnm thường xuyên ạ
Khoảng trước 9h tôi ở tổ Giải tích, 305T3. Sau 9h tôi dạy ở 401T4.
thưa thầy,thầy có bài giảng nào về công thức Poisson trên trang này ko ạ?
https://bomongiaitich.wordpress.com/2012/06/02/cong-thuc-poisson-dan-tu-ham-phuc/
https://bomongiaitich.wordpress.com/2012/05/30/cong-thuc-poisson-cong-thuc-tong-poisson/
Lớp K57A1T và K57TN thi cuối kỳ chung một đề. Nội dung gồm:
– bài toán biên hỗn hợp cho phương trình truyền sóng, có dùng đồ thị,
– bài toán biên hỗn hợp cho phương trình truyền nhiệt,
– bài toán biên cho phương trình Laplace,
– nguyên lý cực đại, tích phân năng lượng,
– chú ý ý nghĩa của các điều kiện.
Pingback: Trao đổi bài giảng PTĐHR lớp K58TN | Giải tích
Pingback: Trao đổi bài giảng môn PTĐHR lớp K58A1T | Giải tích