Hôm nay 08/09/2014 tôi bắt đầu dạy Giải tích 1 cho lớp K59A3. Đề cương môn học các bạn xem
Đề cương môn học-Ngành Toan tin-Giai tich 1
Ngoài ra các bạn có thể tham khảo thêm bài trao đổi với lớp K59A3 ở
https://bomongiaitich.wordpress.com/2014/09/08/trao-doi-bai-giang-giai-tich-1-lop-k59a3/
Các bạn có gì cần trao đổi có thể viết vào phần “Phản hồi” ở phía dưới bài viết.
Hôm nay tôi đã nói:
– giáo trình sẽ sử dụng để dạy Giải tích 1,
– đề cương vắn tắt môn học,
– sau đó bắt đầu vào môn học.
Tôi đi qua phần số thực:
– lịch sử sơ qua về số tự nhiên, số 0, số nguyên, số hữu tỷ và số thực,
– điểm phân biệt đáng chú ý giữa tập số hữu tỷ và tập số thực: tiên đề cận trên đúng,
– nói qua về nguyên lý Archimede, các bạn tham khảo thêm
https://en.wikipedia.org/wiki/Archimedean_property
phân biệt với
https://en.wikipedia.org/wiki/Archimedes%27_principle
– tiếp đến tôi trình bày dãy số thực: với khái niệm hội tụ, phân kỳ, giới hạn của dãy số, bị chặn, đơn điệu.
Về dãy số các bạn có thể tham khảo sơ qua trong bài
https://bomongiaitich.wordpress.com/2011/12/02/t%E1%BB%95ng-h%E1%BB%A3p-v%E1%BB%81-day/
đặc biệt bài tổng hợp
Click to access nguyenthihanh1004_nguyenthithanhthuy_k56a2.pdf
Sẽ có lúc tôi cho kiểm tra:
– chứng minh một số, dạng căn thức, là số vô tỷ,
– tìm cận trên đúng và cận dưới đúng của một tập đã cho.
Việc chỉ ra số Euler e và số pi là các số vô tỷ là công việc không dễ, đặc biệt số pi. Các bạn có thể tham khảo bài
https://bomongiaitich.wordpress.com/2013/10/08/so-euler-e-va-so-pi/
Hôm nay 22/09/2015, tôi đã cơ bản trình bày xong phần dãy số thực:
– một số tính chất cơ bản của các dãy hội tụ: tổng, tích, .v.v., của các dãy hội tụ,
– dãy con, giới hạn riêng, giới hạn trên, dưới,
– tiêu chuẩn Cauchy,
– giới hạn bằng vô cùng.
Tôi có nhắc lại về số thực với tính trù mật.
Cuối giờ tôi có đưa ra một số bài tập nhờ một số bạn lên chữa:
– bài về số vô tỷ,
– bài tìm số lớn nhất, số bé nhất,
– bài về ánh xạ đơn ánh, toàn ánh, song ánh,
– bài tập về dãy đơn điệu, bị chặn.
Ngày 22/09/2015 tôi còn nợ các bạn việc chỉ ra dãy
không bị chặn trên.
Ngoài ra việc chứng minh dãy trên là đơn điệu tăng bằng cách lấy đạo hàm là sai! Hàm chỉ tăng trong từng chu kỳ của nó!!! Có thể nói dãy trên không tăng, không giảm:
chỉ tăng trong từng chu kỳ của nó!!! Có thể nói dãy trên không tăng, không giảm:
Như tôi đã nói trên lớp:
Bạn nào viết hoàn chỉnh chứng minh
“Chỉ ra dãy con của dãy là dãy hội tụ.$”
là dãy hội tụ.$”
tôi sẽ cho bạn đó 10,0 điểm giữa kỳ.
Một bài cũng tương tự với tính chất như vậy, nghĩa là: tôi cũng sẽ cho 10,0 điểm thường xuyên bạn nào đưa ra chứng minh hoàn chỉnh:
“Chỉ ra dãy con của dãy hội tụ đến
hội tụ đến  .”
.”
Tôi có đưa ra cách chứng minh bằng phản chứng rằng dãy phân kỳ. Trong cách chứng minh đó tôi có sử dụng “điều kiện cần” sau:
phân kỳ. Trong cách chứng minh đó tôi có sử dụng “điều kiện cần” sau:
Nếu dãy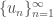 hội tụ thì
hội tụ thì
với mọi số tự nhiên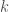 cố định ta đều có
cố định ta đều có
Chú ý đây chỉ là điều kiện cần (nesessary condition) chứ không phải điều kiện đủ (sufficient condition), nghĩa là
nếu hội tụ thì “điều kiện” xảy ra,
và
nếu “điều kiện” xảy ra thì chưa chắc hội tụ.
Tôi đã lấy ví dụ dãy phân kỳ
mà điều kiện cần vẫn xảy ra.
Một cách khác chứng minh dãy phân kỳ có thể xem
phân kỳ có thể xem
http://math.stackexchange.com/questions/260766/divergence-of-the-sequence-sinn?lq=1
Trong cách này có sử dụng tính “trù mật” của tập số tự nhiên trong tập các số thực dương theo nghĩa:
với bất kỳ hai số thực dương thỏa mãn
thỏa mãn 
ta đều tìm được số tự nhiên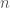 sao cho
sao cho
Nó khác tính trù mật của tập số hữu tỷ trong tập số thực ở điểm
Không khó để thấy
Ta có thể dùng nguyên lý kẹp (tôi chưa dạy cho K60A3). Các bạn có thể tham khảo
https://en.wikipedia.org/wiki/Squeeze_theorem
Tuy nhiên dãy
lại rất khác.
Ngày 29/09/2015 tôi nhắc lại một số tính chất về dãy số:
– đặc biệt lưu ý chỉ có: giới hạn của tổng bằng tổng các giới hạn, khi các giới hạn tồn tại,
– bổ sung nguyên lý so sánh, từ đó dẫn đến nguyên lý kẹp, đây chính là một trong các biểu hiện của nguyên lý Cantor về dãy lồng nhau, thắt lại,
– tôi có nói về Định lý Heine-Borel, nhưng thực chất tôi nói về phát biểu tương đương Định lý Bolzano-Weierstrass, các bạn có thể xem
https://en.wikipedia.org/wiki/Heine%E2%80%93Borel_theorem
https://en.wikipedia.org/wiki/Bolzano%E2%80%93Weierstrass_theorem
Sau đó tôi có trình bày giới hạn hàm số: cho hàm một biến và hàm hai biến:
– điểm tụ, điểm cô lập,
– giới hạn của hàm số tại điểm tụ,
– tính chất của giới hạn hàm số,
– mối quan hệ giữa dãy số và giới hạn hàm số, ứng dụng vào việc tính giới hạn dãy số và chứng minh không có giới hạn
và chứng minh không có giới hạn 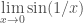 ,
,
– tính liên tục của hàm số.
Cuối giờ tôi cho bài kiểm tra ngắn:
1. Chứng minh rằng
2. Xét tập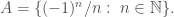 Tính
Tính 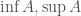 .
.
Ngày 29/09/2015 tôi có đưa ra một số ví dụ để thấy chưa chắc có
Những ví dụ đó đều có hiện tượng
cả hai dãy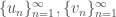 phân kỳ.
phân kỳ.
Một tình huống khác giới hạn của tích cũng được nhắc đến: chưa chắc có giới hạn của dãy tích bằng tích các giới hạn. Một điều trùng hợp: “tích” của hai số vô tỷ chưa chắc vô tỷ. Nhưng một số bạn làm bài kiểm tra ngắn cuối giờ, sau khi chỉ ra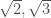 là các số vô tỷ dẫn đến
là các số vô tỷ dẫn đến 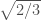 là số vô tỷ. Lập luận này là không đúng! Vì nếu đúng thì
là số vô tỷ. Lập luận này là không đúng! Vì nếu đúng thì 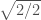 là số vô tỷ!?!
là số vô tỷ!?!
Một số lưu ý về những tình huống kiểu này các bạn xem
https://bomongiaitich.wordpress.com/2014/09/08/trao-doi-bai-giang-giai-tich-1-lop-k59a3/#comment-3206
06/10/2015 tôi bắt đầu bằng việc chữa bài kiểm tra ngắn lần trước, rồi nhờ một số bạn lên chữa các bài về tính đơn điệu, bị chặn của dãy số cũng như chứng minh điểm tụ, điểm cô lập của một tập.
Tiếp đến tôi trình bày:
– hàm một biến: giới hạn trái, giới hạn phải, gián đoạn loại I, loại II, hàm đơn điệu, hàm bị chặn,
– hàm hai biến: giới hạn lặp, giới hạn kép,
– tiêu chuẩn Cauchy, dấu hiệu đơn điệu và bị chặn dẫn đến có giới hạn,
– nhắc lại vài tính chất của giới hạn hàm số, bổ sung tính bảo toàn thứ tự và nguyên lý kẹp,
– hàm một biến: giới hạn tại vô cùng và giới hạn bằng vô cùng,
– khái niệm VCL, VCB của hàm số một biến tại điểm tụ.
Tuần tới tôi tiếp tục phần VCL, VCB rồi chuyển sang tính chất của hàm liên tục.
Về tính đơn điệu các bạn tham khảo
https://bomongiaitich.wordpress.com/2013/11/08/tinh-don-dieu/
Về giới hạn kép các bạn tham khảo
https://bomongiaitich.wordpress.com/?s=gi%E1%BB%9Bi+h%E1%BA%A1n+k%C3%A9p
Về VCL, VCB các bạn tham khảo
https://bomongiaitich.wordpress.com/2011/11/09/vo-cung-l%E1%BB%9Bn-vo-cung-be/
Tôi nói chưa đúng về dấu hiệu đơn điệu và bị chặn của giới hạn hàm số một biến:
Xét hàm một biến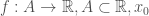 là điểm tụ của
là điểm tụ của 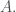
Nếu có số sao cho
sao cho
thì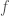 có giới hạn tại
có giới hạn tại 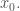
Phát biểu trên không đúng. Quan sát các ví dụ sau:
VD1: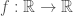 xác định bởi
xác định bởi
là hàm đơn điệu tăng, bị chặn trong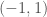 và
và
VD2: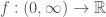 xác định bởi
xác định bởi
là hàm đơn điệu tăng, bị chặn trên bởi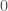 và
và
Ta phải thêm giả thiết lên tập tập
tập 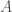 nằm bên trái điểm
nằm bên trái điểm 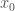 , nghĩa là
, nghĩa là
thầy nói lại chỗ phân loại hàm gián đoạn được không ạ?chỗ loại 1 và loại 2 và trong loại 1 có 2 loại con đấy ạ
Xét hàm một biến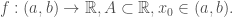
TH1: tồn tại giới hạn của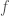 tại
tại 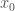 và
và
ta nói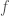 có gián đoạn loại I khử được tại
có gián đoạn loại I khử được tại 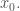
VD: xác định bởi
xác định bởi
có gián đoạn loại I khử được tại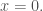
TH2: có giới hạn trái và giới hạn phải của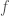 tại
tại 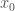 và
và
ta nói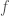 có gián đoạn loại I không khử được tại
có gián đoạn loại I không khử được tại 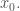
VD: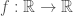 xác định bởi
xác định bởi
có gián đoạn loại I không khử được tại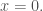
TH3: tại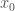 hàm
hàm 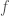 không có giới hạn trái, hoặc không có giới hạn phải hoặc không có cả hai ta nói
không có giới hạn trái, hoặc không có giới hạn phải hoặc không có cả hai ta nói 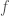 có gián đoạn loại II tại
có gián đoạn loại II tại 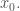
VD: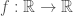 xác định bởi
xác định bởi
có gián đoạn loại II tại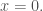
Thầy cho em xin đề kiểm tra giữa kì I các khóa trước ạ
Em vào chuyên mục đề thi
https://bomongiaitich.wordpress.com/category/d%E1%BB%81-thi/
sẽ tìm thấy đề thi các năm trước. Đặc biệt K58A2+A3, K59A2+A3 có nội dung môn học giống K60A3.
Em chỉ thấy đề cuối kì thôi ạ
Click to access decuoikygt1_2014.pdf
Click to access giaitich1_khmt2013.pdf
Không có đề giữa kì hả thầy???
Em xem bài ngày 05 tháng 11 năm 2014.
Hôm nay 13/10/2015 tôi bắt đầu bằng việc cho các bạn làm quen với:
– giới hạn riêng, điểm tụ, điểm cô lập, gián đoạn
– giới hạn trái, giới hạn phải, giới hạn kép.
Sau đó tôi sửa lại kết quả về đơn điệu và bị chặn của giới hạn hàm số. Từ đó dẫn đến: hàm đơn điệu chỉ có gián đoạn loại I.
Tôi nói tiếp về VCL, VCB:
– bậc cao hơn, cùng bậc,
– tương đương và kỹ thuật thay thế VCB tương đương khi tính giới hạn hàm số.
Tiếp đến tôi chuyển sang các tính chất của hàm liên tục:
– các phép tuyến tính, phép nhân, phép chia,
– phép hợp thành.
Sau đó tôi chuyển sang một số tính chất của hàm liên tục trên![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=444444&s=0&c=20201002) và
và ![[a, b]\times[c, d]:](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D%5Ctimes%5Bc%2C+d%5D%3A&bg=ffffff&fg=444444&s=0&c=20201002)
– tính bị chặn, đạt giá trị lớn nhất, nhỏ nhất,
– tính liên thông.
Cuối giờ tôi cho bài kiểm tra ngắn:
1. Xét dãy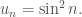
a (4 điểm). CMR: (-1/2) không là giới hạn riêng của dãy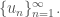
b. (Cộng điểm: 2 điểm) CMR: tập các giới hạn riêng của dãy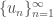 nằm trong [0, 1].
nằm trong [0, 1].
2. Xét tập![A=[-1, 1]\times[-1, 1]\cup\{(2, 0)\}.](https://s0.wp.com/latex.php?latex=A%3D%5B-1%2C+1%5D%5Ctimes%5B-1%2C+1%5D%5Ccup%5C%7B%282%2C+0%29%5C%7D.&bg=ffffff&fg=444444&s=0&c=20201002)
a. (3 điểm) CMR: (0, 0) là điểm tụ của A.
b. (3 điểm) CMR: (2, 0) là điểm cô lập của A.
Hôm nay 20/10/2015 tôi bắt đầu bằng việc chữa bài kiểm tra ngắn tuần trước:
– các bạn có thể làm câu 1 bằng việc dùng tính bảo toàn thứ tự của giới hạn dãy số,
– cách bọc điểm (-1/2) “rời khỏi” dãy đang xét giống như cách bọc điểm (2, 0) “rời khỏi” phần còn lại của tập đang xét.
Sau đó tôi có nhờ một số bạn chữa bài tập:
– về hàm được cho bởi các công thức khác nhau,
– hàm hợp,
– giới hạn lặp.
Sau đó tôi quay trở lại hàm liên tục một biến và nhiều biến, đặc biệt với hàm một biến ta có các kết quả:
– Nếu![f: [a, b]\to\mathbb R](https://s0.wp.com/latex.php?latex=f%3A+%5Ba%2C+b%5D%5Cto%5Cmathbb+R&bg=ffffff&fg=444444&s=0&c=20201002) là hàm đơn điệu thì
là hàm đơn điệu thì
khi và chỉ khi
– Nếu![f:[a, b]\to\mathbb R](https://s0.wp.com/latex.php?latex=f%3A%5Ba%2C+b%5D%5Cto%5Cmathbb+R&bg=ffffff&fg=444444&s=0&c=20201002) là hàm liên tục, đơn ánh thì
là hàm liên tục, đơn ánh thì
+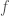 là hàm đơn điệu,
là hàm đơn điệu,
+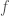 là song ánh từ
là song ánh từ ![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=444444&s=0&c=20201002) vào
vào ![f([a, b])](https://s0.wp.com/latex.php?latex=f%28%5Ba%2C+b%5D%29&bg=ffffff&fg=444444&s=0&c=20201002) ,
,
+ ánh xạ ngược![f^{-1}: f([a, b])\to[a, b]](https://s0.wp.com/latex.php?latex=f%5E%7B-1%7D%3A+f%28%5Ba%2C+b%5D%29%5Cto%5Ba%2C+b%5D&bg=ffffff&fg=444444&s=0&c=20201002) là hàm liên tục.
là hàm liên tục.
Tôi cũng đưa ra các ví dụ cho thấy các kết quả trên sai khi bỏ đi một trong các giả thiết.
Tôi kết thúc phần giới hạn hàm số và hàm liên tục bằng một vài hàm cơ bản và các VCL ở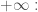
và tính liên tục theo từng biến của hàm hai biến.
Sau đó tôi chuyển sang khái niệm khả vi:
– điểm trong, tập mở,
– hàm khả vi tại điểm trong tập mở,
– đạo hàm trái, phải.
Cuối cùng tôi đưa ra ví dụ về hàm cho bởi nhiều công thức.
Hôm nay, 27/10/2015, tôi tiếp tục phần phép tính vi phân của hàm số:
– một số tính chất: đạo hàm hàm tổng, hàm tích, hàm thương, hàm hợp của hàm một biến và hàm nhiều biến,
– chú ý đạo hàm tại một điểm của hàm một biến là một số, hàm nhiều biến là một véc-tơ,
– hàm nhiều biến khả vi thì nó có đạo hàm riêng và đạo ánh tại một điểm là véc-tơ gồm các đạo hàm riêng tại đó,
– ví dụ về hàm có đạo hàm riêng và không khả vi,
– tiếp đến là Định lý Fermat về cực trị địa phương, Định lý Rolle, Định lý Lagrange, Định Cauchy và sơ qua về L’Hopital.
Cuối giớ tôi cho kiểm tra ngắn:
1. Xét dãy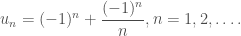
(a) (4 điểm) CMR: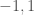 là giới hạn riêng của dãy
là giới hạn riêng của dãy 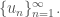
(b) (Cộng 2 điểm) CMR:
2. Cho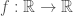 xác định bởi
xác định bởi
(a) (3 điểm) Tìm tất cả để
để 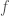 liên tục trên
liên tục trên 
(b) (3 điểm) Tìm tất cả để
để 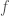 khả vi tại
khả vi tại 
Khi nói về Định lý Fermat về cực trị tôi có nói về Định lý Fermat:
Không có các số nguyên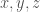 để
để
với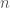 là số tự nhiên,
là số tự nhiên, 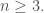
Các bạn xem
https://en.wikipedia.org/wiki/Fermat%27s_Last_Theorem
Để chứng minh Định lý Fermat cần đến đường cong đại số. Đường cong đại số dẫn đến kỹ thuật mật mã,
Click to access 2012-Curves-Crypto-with-Exercises.pdf
Tôi cũng nói đến mật mã hình vuông. Các bạn xem
https://en.wikipedia.org/wiki/Polybius_square
https://en.wikipedia.org/wiki/Four-square_cipher
Các kỹ thuật mật mã trên liên quan đến đại số và số học. Kỹ thuật mật mã liên quan đến giải tích, cụ thể sóng nhỏ các bạn xem
Click to access 20110427.pdf
Bài 1 câu b, trong đề kiểm tra ngắn, một số bạn tách dãy đã cho thành hai dãy con chẵn và lẻ, rồi tính được giới hạn hai dãy con này. Từ đó kết luận đó là tất cả các giới hạn riêng của dãy ban đầu. Làm như này chưa đầy đủ. Chẳng hạn: chưa trả lời được câu hỏi tại sao những số khác hai giới hạn riêng tìm được lại không là giới hạn riêng của dãy đã cho?
Để cụ thể tôi xét ví dụ sau:
Cho dãy khi
khi 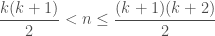 với
với 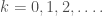
Ta liệt kê mười số đầu tiên của dãy:
Với mỗi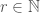 cố định xét dãy con
cố định xét dãy con
Không khó để thấy:
+)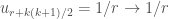 khi
khi 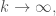
+) các dãy con này phủ kín dãy ban đầu.
Vậy tập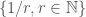 có phải là tất cả các giới hạn riêng của dãy đã cho?
có phải là tất cả các giới hạn riêng của dãy đã cho?
03/11/2015 tôi bắt đầu bằng việc chữa bài kiểm tra ngắn. Một câu hỏi nhỏ từ bài kiểm tra ngắn:
– liệu đẳng thức
có đúng không?
Tiếp theo tôi có nhờ một số bạn lên tính đạo hàm riêng và khảo sát tính khả vi của hàm hai biến.
Sau đó tôi nhắc lại Định lý Fermat cho hàm một biến và hai biến, Định lý Lagrange cho hàm một biến và hai biến, đặc biệt với hàm véc-tơ “không có” Định lý Lagrange. Tôi chuyển qua Định lý hàm ngược cho hàm một biến, rồi hàm véc-tơ hai biến. Tiếp đến tôi nói về phép tính vi phân cấp 1.
Cuối giờ tôi cho bài kiểm tra ngắn:
Xét hàm
(a) (6 điểm + 2 điểm) Tính các đạo hàm riêng
(b) (2 điểm) Hỏi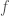 có khả vi tại điểm
có khả vi tại điểm 
Em chào Thầy, Thầy ơi vừa rồi em có đọc lại một tài liệu về phép tính vi phân hàm một biến và có đọc một dòng giới thiệu : ” Tư tưởng cơ bản của phép tính vi phân là thay hàm đã cho trong một lân cận điểm nào đó bởi một hàm tuyến tính với các sai số là vô cùng bé bậc cao hơn so với số gia tương ứng của đối số ” . Em không hiểu là việc thay mà lời giới thiệu đề cập tới có phải là ở chỗ : Nếu f là hàm có đạo hàm thì đenta(y) = f (x+ đenta x) – f(x) = f ‘ (x) . đenta x + vô cùng bé bậc cao hơn so với đenta x , khi đó f ‘ (x) . đenta x là vi phân của f tại x . Nếu như thế này thì vi phân thay thế cho đenta y chứ sao lại nói là : thay hàm đã cho trong một lân cận điểm nào đó bởi một hàm tuyến tính với các sai số là vô cùng bé bậc cao hơn so với số gia tương ứng của đối số ạ , Thầy có thể giải thích cho em hiểu được không ạ , em cám ơn Thầy .
Tôi nghĩ họ ký hiệu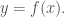
Dạ , đúng là y = f(x) . Em vẫn chưa hiểu ý Thầy ạ , nếu y = f(x) thì ta có điều gì ạ ??
Quanh điểm thay vì hàm
thay vì hàm 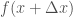 (biến
(biến 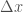 ) ta xét hàm tuyến tính
) ta xét hàm tuyến tính
Hàm tuyến tính sai khác so với hàm đã cho một VCB bậc cao hơn
Hôm nay 10/11/2015 tôi chữa bài kiểm tra tuần trước với các chú ý:
– để hàm nhiều biến khả vi thì nó phải có đạo hàm riêng,
– để chứng minh hàm không có giới hạn thì phải chọn hai dãy .v.v..
Tiếp đến tôi quay lại phép vi phân:
– chứng minh hình thức Định lý hàm ẩn cho đường cong trong mặt phẳng, trong không gian, và mặt cong trong không gian,
– đạo hàm cấp cao, vi phân cấp cao hàm một biến và công thức Leibniz.
Tiếp đến tôi nói về đạo hàm theo hướng của hàm hai biến và mối liên hệ với đạo hàm riêng.
Sau đó tôi trình bày công thức Taylor cho hàm một biến với các phần dư dạng:
– Peano: vô cùng bé,
– Lagrange, Cauchy: đạo hàm cấp cao tại điểm trung gian.
Sử dụng công thức Taylor:
– xác định cực trị địa phương, điểm uốn,
– đưa ra các vô cùng bé tương đương,
– chứng minh một số bất đẳng thức.
Tôi nói qua về L’Hopital cho hàm số. Lúc đó tôi có nói đến dạng tương tự cho dãy số, Bổ đề Stolz hay còn gọi Định lý Stolz-Cesaro:
Cho hai dãy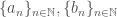 thỏa mãn:
thỏa mãn:
+) dãy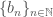 tăng thực sự, nghĩa là
tăng thực sự, nghĩa là 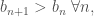 và tiến ra vô cùng, (trên lớp tôi nhầm là hai dãy tiến về 0)
và tiến ra vô cùng, (trên lớp tôi nhầm là hai dãy tiến về 0)
+) tồn tại giới hạn
Khi đó tồn tại giới hạn
Với hàm số ta ngoài dạng 0/0, ta cũng có L’Hopital tương tự như trên:
Cho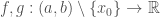 là các hàm khả vi,
là các hàm khả vi, 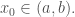 Giả sử:
Giả sử:
+)
+) tồn tại để
để 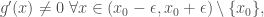 (tính đơn điệu chặt gần
(tính đơn điệu chặt gần 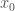 ),
),
+) tồn tại giới hạn
Khi đó tồn tại giới hạn
Ví dụ sử dụng Stolz-Cesaro:
Tính giới hạn
Lấy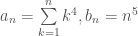 có
có
+)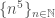 tăng thực sự ra vô cùng,
tăng thực sự ra vô cùng,
+)
Giới hạn cần tính bằng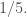
Các bạn có thể tham khảo thêm về L’Hopital và Stolz-Cesaro ở
https://en.wikipedia.org/wiki/L%27H%C3%B4pital%27s_rule
https://en.wikipedia.org/wiki/Stolz%E2%80%93Ces%C3%A0ro_theorem
Về hàm lồi các bạn tự đọc trong sách hoặc
https://en.wikipedia.org/wiki/Convex_function
Ví dụ về hàm có đạo hàm theo mọi hướng và không có mối quan hệ giữa đạo hàm theo hướng và đạo hàm riêng:
Xét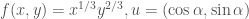 có
có
Lấy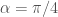 ta thấy
ta thấy
Chú ý khi sử dụng L’Hopital:
Nếu giới hạn của thương của đạo hàm không tồn tại thì không biết gì về giới hạn của thương.
Dưới đây là một vài ví dụ:
VD1: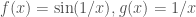 và
và 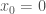 có
có
+) khi
khi 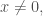
+)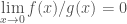 ,
,
+)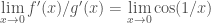 không tồn tại.
không tồn tại.
VD2: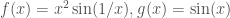 và
và 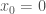 , có
, có
+)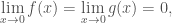
+)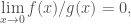
+)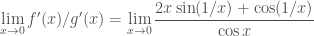 không tồn tại.
không tồn tại.
Hôm qua tôi có tính dở khai triển Taylor tại x=0 của hàm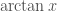 . Các bạn có thể dùng máy tính như sau
. Các bạn có thể dùng máy tính như sau
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427eovrdrtsesb
Tham khảo thêm về khai triển Taylor
https://en.wikipedia.org/wiki/Taylor_series
Một ví dụ vừa dùng Stolz-Cesaro và L’Hopital:
Tính
Giới hạn này liên quan đến hằng số Euler-Mascheroni
Các bạn có thể tham khảo
https://en.wikipedia.org/wiki/Euler%E2%80%93Mascheroni_constant
Hôm nay, 17/11/2015, tôi bắt đầu bằng việc nhờ một số bạn lên chữa các bài tập về:
– tính vi phân cấp 1, cấp 2 của hàm dạng ẩn, dạng tham số,
– tính đạo hàm theo hướng.
Chẳng hạn tính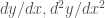 khi
khi
Có
Một bạn lên tính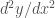 như sau:
như sau:
nên
So với cách tính của tôi
Vậy cách nào đúng? Lý do?
Cách tôi làm đúng, cách bạn kia làm còn thiếu!
Cụ thể:
Khi là biến thực sự (không là hàm của biến nào) thì
là biến thực sự (không là hàm của biến nào) thì
Trong trường hợp này
nên
Các bạn thử hoàn thiện phần còn lại?
Tiếp đến tôi có nói đến việc sử dụng khai triển Taylor để tính gần đúng chẳng hạn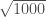 .
.
Sau đó tôi chuyển sang hàm nhiều biến:
– đạo hàm riêng cấp 2, Định lý Schwarz về tính đối xứng,
– khai triển Taylor đến cấp 2,
– dùng tính xác định dương, xác định âm và đổi dấu của ma trận Hessian để xem điểm dừng là cực tiểu địa phương, cực đại địa phương, điểm yên ngựa (một cách tương ứng),
– chú ý có TH ta không dùng được cách trên để xem điểm dừng thuộc loại nào, tuy nhiên vẫn có thể trực tiếp kiểm tra, chẳng hạn hàm ,
,
– cực trị có điều kiện.
Như vậy tôi đã kết thúc phần phép tính vi phân. Tuần tới tôi chuyển sang phép tính tích phân hàm một biến.
Cuối giờ tôi cho kiểm tra ngắn:
1. Xét hàm
Tính đạo hàm theo hướng trong đó
trong đó  hợp với chiều dương trục
hợp với chiều dương trục  một góc
một góc 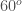 , tại điểm
, tại điểm  .
.
2. (a) Tính các vi phân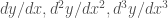 của
của
(b) Khai triển Taylor đến cấp 3 hàm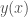 , ở câu (a), tại điểm
, ở câu (a), tại điểm 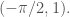
Thang điểm: 1 (3 điểm), 2a (4 điểm + 3 điểm + 2 điểm), 2b (2 điểm).
thầy nói lại cách tính d^2y/dx^2 với hàm không theo tham số được không ạ?
Lấy bài kiểm tra vừa rồi để thực hành
Lấy vi phân hai vế
nên
C1: Tiếp tục lấy vi phân (2) với chú ý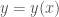 .
.
C2: Lấy vi phân (1), với chú ý là biến thực sự nghĩa là
là biến thực sự nghĩa là  ,
,
nên
Bạn tự hoàn chỉnh nhé.
Thầy tính giúp em câu giới hạn này ạ: lim sinx.tanx/x^2 khi x->0
Chú ý
Viết lại giới hạn cần tính
Bạn tự hoàn thiện nhé.
24/11/2015 tôi bắt đầu bằng việc chữa bài kiểm tra ngắn tuần trước. Sau đó tôi nhờ một số bạn lên tìm cực trị, cực trị có điều kiện. Tôi có nói về việc dùng wolframalpha.com để vẽ đồ thị:
– hàm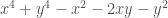
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427en0qdkjmr19
– hàm
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427e9jm0l17ohm
Tiếp theo tôi nói về nguyên hàm với chú ý:
– nguyên hàm của 0,
– nguyên hàm của hàm xác định từng đoạn,
– nguyên hàm của hàm xác định trên các khoảng mở rời nhau,
– cách tính: đổi biến, tích phân từng phần, tích phân hàm hữu tỷ.
Tôi có tính thử nguyên hàm
Dùng wolframalpha.com
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427eb6l3qrgovm
với hàm ngược
Các bạn tự đọc tính nguyên hàm
– hàm hữu tỷ,
– hàm chứa căn thức,
– hàm nhị thức,
– hàm lượng giác.
Vài điểm lưu ý
– không phải hàm nào cũng có nguyên hàm,
– có những hàm có nguyên hàm không tính được dưới dạng hàm cơ bản.
Câu hỏi rất khó:
– hàm có đặc trưng gì thì có nguyên hàm?
– hàm có đặc trưng gì thì có nguyên hàm viết được dưới dạng hàm cơ bản?
Bài xét cực trị hàm
tại điểm (0, 0)
có dạng toàn phương
Tôi có kết luận trên lớp (0, 0) là điểm cực đại địa phương. Kết luận này sai!
Nếu nhìn trên đường x=-y:
còn theo đường x=y
nên kết luận đúng phải là
(0, 0) là điểm yên ngựa.
01/12/2015 tôi bắt đầu bằng việc sửa lại lỗi sai của bài cực trị tuần trước. Tiếp đến tôi nhờ một số bạn lên tìm nguyên hàm của các hàm hữu tỷ, hàm chứa căn, hàm nhị thức. Tuần tới tôi sẽ chữa các bài liên quan đến hàm lượng giác.
Sau đó tôi chuyển sang tích phân xác định với ví dụ:
– hàm khả tích và không có nguyên hàm,
– hàm không bị chặn thì không khả tích,
– hàm bị chặn và không khả tích,
– tính tích phân xác định bằng định nghĩa.
Tôi tiếp tục chuyển sang một số tính chất của tích phân xác định:
– tuyến tính,
– chia miền,
– tính khả tích của hàm tích, hàm min, hàm max, hàm trị tuyệt đối,
– bảo toàn thứ tự,
– Định lý Newton-Leibniz, các bạn có thể tham khảo
https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus
– các Định lý giá trị trung bình.
Về Định lý giá trị trung bình các bạn có thể tham khảo thêm
https://bomongiaitich.wordpress.com/2014/12/09/dinh-ly-gia-tri-trung-gian-dinh-ly-gia-tri-trung-binh-dinh-ly-pappus/#more-3580
https://bomongiaitich.wordpress.com/2011/12/22/ph%E1%BA%A7n-d%C6%B0-trong-cong-th%E1%BB%A9c-taylor-d%C6%B0%E1%BB%A3c-d%E1%BA%ABn-t%E1%BB%AB-d%E1%BA%B3ng-th%E1%BB%A9c-tich-phan/
Một vài tích phân không xác định đã chữa tính bởi wolframalpha.com
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427e745ds4crl1
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427ek5ol6k6ti
http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427evok2ut7or
Hôm nay 08/12/2015 tôi bắt đầu bằng bài kiểm tra ngắn:
Câu 1: (5 điểm) Tìm cực trị của hàm
Câu 2: (5 điểm) Tìm GTLN, GTNN của hàm
với điều kiện
Sau đó tôi nhắc lại Định lý cơ bản của phép tính vi-tích phân với lưu ý:
– sử dụng nguyên hàm để tích tích phân xác định, đặc biệt phép đổi biến,
– sử dụng tích phân xác định để tính nguyên hàm.
Tiếp đến tôi có nói về việc sử dụng tổng tích phân để:
– tính giới hạn dãy số bằng tích phân xác định,
– thiết lập công thức tính diện tích của miền nằm giữa hai đồ thị, miền quạt trong tọa độ cực,
– thiết lập công thức tính độ dài đường cong,
– thiết lập công thức tính diện tích xung quanh, thể tích của hình tròn xoay.
Tôi chuyển sang phần tích phân suy rộng:
– với ví dụ về tính toán cụ thể hàm Gamma,
– định nghĩa khái niệm hội tụ, phân kỳ,
– tiêu chuẩn Cauchy,
– dấu hiệu so sánh.
Cuối giờ tôi cho bài kiểm tra ngắn thứ hai:
Câu 1. (6 điểm) Cho xác định bởi
xác định bởi
Tính tích phân không xác định .
.
Câu 2. (4 điểm) Cho đường cong
Tính diện tích miền được bao quanh bởi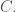
15/12/2015, tôi bắt đầu bằng việc chữa hai bài kiểm tra ngắn tuần trước với chú ý:
– bài tìm cực trị, khi ta không nhận biết được điểm dừng là cực trị hay không bằng việc sử dụng đạo hàm riêng cấp 2 thì ta phải quay trở lại nhìn hàm đã cho và xét trực tiếp,
– bài tìm GTLN, GTNN, khi tìm được điểm dừng ta không cần xét đạo hàm riêng cấp 2 mà so sánh giá trị của hàm tại các điểm dừng và điểm biên,
– bài tìm nguyên hàm có hai cách: dùng tích phân xác định với cận thay đổi, hay tính nguyên hàm trên từng đoạn, nhớ chú ý các hằng số,
– bài tính diện tích miền cho bởi hệ tọa độ cực chú ý miền của góc quay.
Tiếp đến tôi có nhờ một số bạn tính đạo hàm, giới hạn của các tích phân xác định có cận thay đổi (tích phân phụ thuộc tham số) với chú ý việc sử dụng Newton-Leibniz và đạo hàm hàm hợp.
Sau đó tôi quay trở lại tích phân suy rộng với:
– ví dụ về việc dùng tiêu chuẩn Cauchy chứng minh tích phân suy rộng phân kỳ, hội tụ,
– tính toán cụ thể một vài tích phân suy rộng bằng định nghĩa.
Cuối giờ tôi nhờ một số bạn lên tính nguyên hàm, tích phân xác định, tích phân suy rộng. Các bạn chú ý các kỹ năng tính nguyên hàm của:
– hàm hữu tỷ,
– hàm chứa căn thức,
– hàm dạng nhị thức,
– hàm lượng giác.
Ngoài ra việc tính tích phân suy rộng chú ý việc tách tích phân thành tổng hai tích phân suy rộng.
Tuần tới là buổi tôi dành để trả lời các câu hỏi về môn học. Các bạn xem lại những gì đã học và chuẩn bị các câu hỏi.
thầy cho e hỏi trên trang wolframalpha gõ tích phân như thế nào ạ?
Tích phân gõ
int
(viết tắt integral).
Nếu tích phân có cận dưới a, cận trên là b, thì gõ
int_a^b
Chẳng hạn tìm nguyên hàm
gõ
int \sin(x^2)dx
Còn tính tích phân xác định
gõ
int_0^x \sin(t^2)dt
Buổi cuối cùng, một số bạn lên chữa các bài kiểm tra cuối kỳ K58 và K59. Sau đó một số bạn chữa một số bài ứng dụng tích phân xác định tính
– độ dài đường cong: tham số hóa, nghĩa là viết các tọa độ x, y là hàm theo cùng một biến, chẳng hạn t, xác định miền chạy của t, từ đó lắp vào công thức tính độ dài đường cong là tích phân xác định với cận là miền chạy biến t,
– diện tích miền nằm giữa hai đường cong: viết các đường cong dưới dạng hàm y=y(x), xác định giao điểm các đường cong, từ đó lắp vào công thức tính diện tích là tích phân xác định với cận là các hoành độ của giao điểm,
– thể tích của vật thể: cắt vật thể thành các lát mỏng bởi các mặt phẳng vuông với trục 0x, tính thiết diện mỗi lát mỏng, lắp vào công thức tính thể tích với cận tích phân là điểm xuất phát và điểm cuối của hai mặt phẳng vuông góc chạm vào vật.