29/11/2015 tôi bắt đầu dạy môn PTĐHR cho lớp CH2016-2018.
Đề cương của môn học các bạn xem file
Về quá trình học các bạn tham khảo thêm
https://bomongiaitich.wordpress.com/2015/12/01/trao-doi-bai-giang-mon-ptdhr-lop-ch2015-2017/
Có gì cần trao đổi các bạn viết vào phần phản hồi.
Các bạn có thể làm các bài tập về việc giải bài toán Cauchy cho PT cấp 1 trong quyển “A basic course in PDEs”.
Ngoài cuốn của Q. Han các bạn có thể tham khảo:
– bài tập cuối Chương 2 cuốn “An introduction to PDEs” của Pinchover-Rubinstein, các bạn lớp TTTN tôi từng dạy đều làm bài tập trong này (trừ K53),
– bài tập trong Chương 8 cuốn “Beginning PDEs” của O’Neil, tôi cho K58TN, K59TN làm.
Bài giảng của tôi về PT cấp 1:
Click to access baigiangptdhr_f0.pdf
Một số bài tìm nghiệm giải tích tại gốc của bài toán Cauchy cho PT cấp 1:
1. Phương trình
với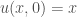 .
.
2. Phương trình
với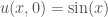 .
.
$\frac{dx}{1}={dy}{-y^2+1}={du}{x.y}$
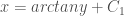
$\frac{x^2.y}{2}=u+C_2$
thầy ơi! thay vì đánh latex e có thể gửi bằng hình ảnh cho thầy xem giúp bài tập giúp e được không ạ! e loay hoay mà k gửi bằng latex được 😦
Được. Cách trước em làm dùng phương pháp đặc trưng. Yêu cầu của các bài này dùng khai triển Taylor để tìm nghiệm.
Nghiệm của bài 1:
Trên lớp tôi tính nhầm
Tôi có thử dùng cách đổi biến, bản chất là phương pháp đặc trưng, thì gặp phải tích phân không xác định
Thoạt nhìn có vẻ dễ?
Bài 2 dùng phép đổi biến
ta dễ dàng tìm được nghiệm
Tìm nghiệm dạng chuỗi của bài 2
thay vào phương trình ta có hệ
và thay vào điều kiện ban đầu
Để ý một chút ta sẽ chỉ ra được
Khi đó
Hôm qua có bạn hỏi tôi về các dạng bài tập PT cấp 1:
– dạng thứ 1: tìm nghiệm dạng chuỗi như tuần trước đã chữa,
– dạng thứ 2: dùng PP đặc trưng, có các hiện tượng:
+ điều kiện Cauchy đặt trên siêu mặt không đặc trưng,
+ điều kiện Cauchy đặt trên siêu mặt đặc trưng: khi đó hoặc bài toán vô nghiệm, hoặc bài toán có vô số nghiệm,
+ hiện tượng sốc: dùng điều kiện Rankine-Hugoniot, đôi khi xử lý hiện tượng chân không.
Các bài tập về sốc các bạn tìm trong
“Applied Partial Differential Equations; with Fourier Series and Boundary Value Problems, Fourth Edition “, R. Haberman,
trong Chapter 12, mục 12.6.
Hôm nay tôi nhờ một số bạn lên chữa hai câu trong bài 2.1, sách Q. Han.
Một bạn dùng phương pháp Lagrange để chữa câu 1, bạn kia dùng đổi biến để chữa câu 2. Cả hai cách đều dẫn đến nghiệm tổng quát.
Hai câu này đều có thể dùng phương pháp Lagrange hay đổi biến. Sau đó tôi có nhờ hai bạn lên tìm nghiệm dạng chuỗi.
Về phương pháp Lagrange không dễ để sử dụng giải bài đầu tôi viết ở trên. Cụ thể
Với bài 1 ta gặp hệ
không dễ để giải theo Lagrange.
Với bài 2 ta gặp
ta giải được
Tại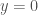 có
có
Hỏi quan hệ với nhau như nào?
quan hệ với nhau như nào?
Trả lời ! (Giải thích?)
! (Giải thích?)
Một số bạn có hỏi tôi về đề thi giữa kỳ. Các bạn tham khảo
https://bomongiaitich.wordpress.com/2016/01/25/de-thi-giua-ky-mon-ptdhr-lop-ch2015-2017/
Chú ý năm ngoái không được dùng tài liệu nên có câu hỏi lý thuyết. Năm nay thi giữa kỳ được sử dụng tài liệu nên sẽ không có lý thuyết mà gồm:
– bài tập tính toán,
– bài tập lý thuyết.
Về phần phương trình cấp 1 có một số bài tập lý thuyết:
– hầu như các bài trong 2.4. Exercises, sách Q. Han, đều là bài tập dạng lý thuyết, rõ nét là các bài 2.3, 2.10, 2.11, 2.12,
– trong Rubinstein-Pinchover có bài tương tự bài 2.3 là bài 2.5 trang 58.
Tôi đã sửa lại một số lỗi trong phần PT cấp 1:
Phương trình cấp 1
Có thêm một số hình vẽ.
Em thưa thầy, thầy có thể giải thích đề câu a, bài 2.5, sách của Qing Han được không ạ ? Em không hiểu ý của đề bài lắm ạ.
Câu a, bài 2.5, yêu cầu tìm các điểm trên đường mà đường đó đặc trưng tại các điểm đó đối với phương trình. Cụ thể hơn, tìm các điểm trên đường
mà đường đó đặc trưng tại các điểm đó đối với phương trình. Cụ thể hơn, tìm các điểm trên đường  mà trường
mà trường  tiếp xúc với đường
tiếp xúc với đường  tại các điểm đó.
tại các điểm đó.
Sau đó tại các điểm này hãy tìm điều kiện tương thích đặt lên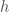 . Điều kiện tương thích xuất hiện khi có mối liên hệ giữa phương trình và điều kiện Cauchy. Chú ý chia trường hợp
. Điều kiện tương thích xuất hiện khi có mối liên hệ giữa phương trình và điều kiện Cauchy. Chú ý chia trường hợp 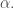
Hôm nay về cơ bản tôi đã trình bày xong phần ôn lại PT cấp 2:
– siêu mặt đặc trưng,
– đánh giá năng lượng ,
– phương pháp tách biến.
Bài giảng phần này:
Click to access baigiangptdhr_r2.pdf
Bài tập phần này:
– tìm nghiệm dạng chuỗi lũy thừa cho bài toán Cauchy cho PT cấp 2,
– phân loại, chuyển về dạng chính tắc, tìm nghiệm tổng quát cho PT cấp 2, sau đó tìm nghiệm thỏa mãn thêm điều kiện đặt trên đường đặc trưng,
– giải nghiệm bài toán biên bằng phương pháp tách biến, dùng lý thuyết để xem nghiệm tách biến có cổ điển không.
Tuần tới tôi trình bày về hàm điều hòa, nghiệm phương trình Laplace. Các bạn lấy tài liệu
Click to access baigiangptdhr_l.pdf
Tôi đã sửa lại phần bài giảng về ôn lại PT cấp 2:
Phương trình cấp 2
Trong đó có bổ sung một số hình vẽ.
Hôm qua tôi có đưa ra bài tìm nghiệm dạng chuỗi của bài toán Cauchy:
Các bạn thử làm chi tiết bài này để tuần tới chữa.
thưa thầy! Thầy có thể cho e xin đáp số của bài tập này được k ạ? E cám ơn thầy a
Chỉ có còn lại hoặc
còn lại hoặc 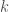 lẻ hoặc
lẻ hoặc  lẻ đều có
lẻ đều có
Từ phương trình
còn từ điều kiện Cauchy
Tính bạn tự làm nhé.
bạn tự làm nhé.
Nghiệm dạng hàm cơ bản:
Vang! E lam đc rồi nh k biết kết quả cuối cùng mình ra đúng k. Nh e so đến đoạn này cũng giống thầy gợi ý rồi a. E cám ơn thầy nhiều
Các bạn thử làm bài 2.8, 2.9, trong Q.Han, về PT phi tuyến hoàn toàn. Tuần tới ta cũng sẽ chữa các bài này.
thưa thầy! e mong thầy có thể nói qua một số bước giải bài toán phi tuyến giúp chúng e ạ. E chưa rõ lắm.
e cám ơn thầy ạ
ví dụ 2.8 về phương trình phi tuyến không hoàn toàn, thầy có thể gợi ý giúp chúng e với ạ.
B1: tham số hóa lại điều kiện Cauchy, chẳng hạn bài 2.8:
B2: giải hệ PT như cuối trang 8 trong giáo trình với chú ý
B3: giải hệ PT (1.2.7)-(1.2.9) với các điều kiện ban đầu ở B1, B2.
Sau khi giải xong B3 ta được nghiệm dạng tham số
B4: giải ngược
B5: thay B4 vào B3 ta được nghiệm
Lúc đầu e làm như bài 2.8 nhưng sau khi giải đến p2(0,t). E thay ngược lại vào dp2/ds tìm p2 thì thấy p2 không tồn tại tại s=0.
E cũng chưa rõ lắm về u(x,1/2×2) liệu có tham số hóa x(0,t)=x0,y(0,t) là đúng hay sai.
Tham số hóa điều kiện Cauchy:
B2: bài 2.8 có hai nghiệm, còn bài 2.9 vô nghiệm.
Thưa thầy có phải 2 nghiệm là ứng với p2(0)=+_1
Dạ vâng.e cám ơn thầy.bài 2.8 e làm được rồi.thầy có thể gợi ý bài 2.9 không ạ.
Em có thể viết B1, B2 cho bài 2.9?
Hôm nay tôi có nói về đề cương thi giữa kỳ:
– Phần PT cấp 1:
+ bài tập tính toán:
– tìm nghiệm dạng chuỗi của bài toán Cauchy khi điều kiện Cauchy đặt trên đường không đặc trưng,
– giải bài toán Cauchy khi điều kiện Cauchy đặt trên đường đặc trưng;
– giải bài toán Cauchy cho PT phi tuyến;
– giải bài toán giá trị ban đầu có hiện tượng sốc;
+ bài tập lý thuyết: liên quan đến chứng minh trong đánh giá;
đánh giá;
– Phần PT cấp 2:
+ bài tập tính toán:
– tìm nghiệm dạng chuỗi của bài toán Cauchy cho PT ellipitic khi điều kiện Cauchy đặt trên đường không đặc trưng;
– phân loại, chuyển về dạng chính tắc, tìm nghiệm tổng quát;
– tìm nghiệm của PT cấp 2 với điều kiện Cauchy đặt trên đường đặc trưng;
– phương pháp tách biến giải bài toán biên hỗn hợp cho PT truyền sóng, truyền nhiệt.
Chú ý về ý nghĩa của các điều kiện biên cho PT truyền sóng, truyền nhiệt.
+ bài tập lý thuyết:
– chỉ ra nghiệm tách biến có cổ điển hay không;
– chỉ ra tính duy nhất nghiệm nhờ tích phân năng lượng,
– đánh giá năng lượng.
Về ý nghĩa điều kiện biên các bạn xem
Click to access y_nghia_dk_ptdhr1.pdf
Thời gian làm bài trong khoảng 50 đến 60 phút.
Dự kiến thi: vào 17/01/2017.
Em chào thầy,
Thưa thầy trong ví dụ cuối cùng của chương 1 có câu: … Nó kết thúc nhiệm vụ của nó tại t= 2 là lúc vùng u = 1 bị chặn lại hoàn toàn…
Thầy có thể cho em hỏi là t = 2 nhìn thấy từ đâu và vùng u = 1 bị chặn như thế nào không ạ ?
Em cảm ơn thầy!
Vùng u=1 nằm giữa đường đặc trưng x=t và đường sốc s_1(t)=1+t/2. Giao điểm của hai đường này là điểm (2, 2) nghĩa là x=2, t=2.
Em chào thầy!
Em muốn hỏi một chút ạ. Trong bài 2 đề 3 giữa kì CH 15-17, pt đã cho là elliptic nên nó có dạng chính tắc là v_xixi+ v_nuynuy=0. Em muốn giải phương trình này để tìm nghiệm Tổng Quát của pt đã cho thì giải ntn ạ?
Chú ý đề bài yêu cầu tìm nghiệm giải tích, nghĩa là tìm nghiệm dạng chuỗi.
Việc tìm nghiệm tổng quát của phương trình này không dễ!
Câu b yêu cầu tìm nghiệm giải tích của bài toán sau đổi biến, còn câu c dùng câu b đưa ra nghiệm của bài toán ban đầu.
Chuyển cả điều kiện Cauchy qua biến \xi, \eta. Sau đó tìm nghiệm dạng chuỗi.
Em thưa thầy, thầy có thể cho chúng em một bài toán tìm nghiệm theo phương pháp tách biến và kiểm tra xem nghiệm đó có là nghiệm cổ điển được không ạ?
Chẳng hạn một số bài trong Pinchover-Rubinstein:
6.14, 6.15, 6.18, 6.20, 7.17.
Tuần sau 17/01/2017 tôi sẽ cho lớp CH16-18 thi giữa kỳ môn PTĐHR. Lớp trưởng cũng như các bạn đã biết nhắc cho các bạn chưa biết giúp tôi nhé.
Về lý thuyết tôi đang dạy PT Laplace:
– nghiệm cơ bản, công thức Green và đồng nhất thức Green,
– hàm Green, công thức nghiệm Poisson cho bài toán biên Dirichlet cho PT Laplace trong hình cầu,
– tính chính quy: nghĩa là độ trơn của hàm điều hòa,
– đánh giá gradient: được chứng minh bởi hai cách, C1 dùng đồng nhất thức Green, C2 dùng công thức giá trị trung bình,
– tính chất trung bình của hàm điều hòa,
– bất đẳng thức Harnack dạng vi phân và bất đẳng thức Harnack, từ đó dẫn đến định lý Liouville về hàm điều hòa trên toàn không gian,
– nguyên lý cực đại.
Tuần sau, tôi lại tiếp tục trình bày nguyên lý cực đại và ứng dụng.
Trong bài giảng hôm nay tôi mắc hai lỗi:
– Lỗi 1: trong quá trình đánh giá gradient, trong bài giảng công thức sau “Thay vào (1.1) ta được …” không có dấu “-“. Trong bản gốc của Q. Han cũng mắc phải lỗi này, cụ thể trang 102, dòng 8 từ trên xuống ở vế phải của công thức “u(x)=…” phải có thêm dấu “-“.
– Lỗi 2: trong quá trình chứng minh tính chất trung bình dẫn đến hàm liên tục là hàm điều hòa tôi gặp
Chỗ này làm rõ thêm bằng việc đổi biến có
có
Từ tính chất giá trị trung bình ta có
thưa thầy. Bọn e vẫn chưa hiểu lắm bài này. Thầy giảng cho chúng e với a. đề bài ux+ u.uy=0
với điều kiện u(x;0)= 1 khi x<0; =2 khi 0<x1. Trong bài này có chân không. Vậy tại x=0; t=0 không là soc phải k thầy?
điều kiện 1 khi x>0
2 khi 0<x1
Đúng vậy (0, 0) là điểm xuất phát của vùng chân không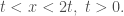 Trong cùng này ta tưởng tượng các đường đặc trưng
Trong cùng này ta tưởng tượng các đường đặc trưng 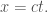 Khi đó nghiệm trong vùng này
Khi đó nghiệm trong vùng này  nối liên tục giữa vùng nghiệm
nối liên tục giữa vùng nghiệm 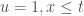 và vùng
và vùng 
Thầy xem giúp em bài này em làm đúng chưa với ạ.
file:///C:/Users/QD/Desktop/IMG_4570.JPG
file:///C:/Users/QD/Desktop/IMG_4571.JPG
file:///C:/Users/QD/Desktop/IMG_4572.JPG
file:///C:/Users/QD/Desktop/IMG_4573.JPG
Thưa thầy, em muốn gửi ảnh bài làm của em thì em phải làm thế nào ạ?
Em đưa file lên mạng rồi gửi đường link. Ví dụ
Tôi lấy ảnh theo đường link “http://blog.kleinproject.org/wp-content/uploads/2013/10/burger1.png”.
Thưa thầy! ví dụ bài toán y.ux+x.uy=y.x
a, u(x,y) =x trên đường y=4x
b, u(x,y)=-2y trên đường y^2 =x^2-2
c, u(x,y) =y^2 trên đường y=-x
e hiểu câu b là bài toán đặt trên đường đặc trưng. Vậy phần a và c có phải dk đặt trên đường đặc trưng không thầy? Vậy có cái nhìn trực quan để phan biệt bài toán nào đặt trên đường đặc trưng hay khong a? E cám ơn thầy ạ
Tích phân phương trình đặc trưng
ta được họ các đường đặc trưng.
Không khó để thấy khi nào điều kiện đặt trên đường đặc trưng hay không?
Thưa thầy! Nếu đề bài yeu cầu xây dựng chuỗi nghiệm của bt truyền nhiệt. Câu hỏi này được hiểu là như thế nào ạ?
Nghĩa là tìm chuỗi nghiệm bằng phương pháp tách biến.
Chiều mai sẽ thi giữa kỳ tại phòng 108T5.
Nếu các bạn đến đầy đủ sớm ta sẽ thi từ 13h00.
Nhờ lớp trưởng và các bạn nhắc các bạn chưa biết.
Hôm nay tôi trình bày gọn phần nguyên lý cực đại mạnh. Có hai điểm thiếu sót trong bài giảng:
– trong chứng minh bổ đề Hopf: “giả thiết thêm” trên mặt cầu
trên mặt cầu 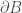 là thừa vì nó được suy ra từ các giả thiết
là thừa vì nó được suy ra từ các giả thiết
– khi phát biểu về bài toán biên Neumann tôi thiếu điều kiện “cầu trong” của biên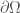 ; giả thiết này là cần thiết vì nếu chỉ có biên thuộc
; giả thiết này là cần thiết vì nếu chỉ có biên thuộc 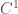 thì có phản ví dụ:
thì có phản ví dụ:
Sabina_Hopf
Các bạn xem thêm về điều kiện cầu trong và độ trơn của biên:
http://math.stackexchange.com/questions/284562/interior-sphere-condition
http://math.stackexchange.com/questions/742771/interior-ball-condition-in-c2-domains?rq=1
Tôi đã sửa và bổ sung hình vẽ vào phần bài giảng phương trình Laplace:
Phương trình Laplace
Phần còn lại của giáo trình, ngoài:
– phương pháp tách biến giải phương trình Laplace,
– công thức D’Alembert cho phương trình truyền sóng,
chủ yếu là các mệnh đề, định lý và các bài tập lý thuyết. Tôi sẽ đánh giá cao việc chữa bài tập lý thuyết. Trước mắt các bạn làm các bài lý thuyết trong bốn đề và các bài cuối chương phần phương trình Laplace trong Q. Han. Ra Tết ta sẽ chữa các bài này.
Ra Tết bắt đầu học trở lại từ chiều thứ Ba, 07/02/2017. Tôi đã hỏi cô Thúy được phòng học cố định 105T5.
thưa thầy! ngoài cách chứng minh ux1x1+ux2x2+….uxnxn=0. ta còn cách nào chứng minh một hàm là điều hòa hả thầy? ví dụ bài đầu tiên trong cuối chương cuốn sách của thầy quing han, nếu u(x) là hàm điều hòa, thì u(x:/x/) có thể hiểu là có dạng j ạ? e gặp khó khăn về vấn đề đạo hàm cấp 1 và cấp 2 của u(x:/x/) thầy ạ!
Còn cách khác: chứng minh hàm thỏa mãn tính chất giá trị trung bình hay thỏa mãn giả thiết của bổ đề Weyl. Có lẽ cách tính đạo hàm là quen thuộc nhất.
vậy nếu e sử dụng đạo hàm thì hàm u(x:/x/) được biểu diễn như thế nào ạ? /x/ là căn (x1^2+….+xn^2) thế còn x: /x/ thì biểu diễn qua x1.x2,…xn thế nào ạ?
Hình như em viết nhầm? Phải là
Có
Tôi có tính toán các đạo hàm riêng sau biến đổi Kelvin trong bài giảng (từ trang 38 đến trang 40):
Click to access ptell.pdf
Cách khác, dùng bổ đề Weyl, nghĩa là phải chứng minh
Đổi biến ta cần chứng minh
ta cần chứng minh
Tôi đã sửa lại bài giảng về phương trình truyền nhiệt:
– một số nhờ bạn N.P.Minh chỉ,
– và lỗi trong tính chất trung bình trên mặt cầu nhiệt.
Các bạn so sánh
Đường link đến bản cũ
và
Phương trình truyền nhiệt (mới sửa lại)
Phần phương trình Laplace còn khoảng bốn giờ nữa, sau đó tôi sẽ chuyển sang phương trình truyền nhiệt. Về cơ bản phương trình truyền nhiệt có nhiều nét giống phương trình Laplace. Có điểm khác biệt khá rõ:
– với phương trình Laplace chỉ có siêu mặt không đặc trưng,
– với phương trình truyền nhiệt điều kiện ban đầu đặt ngay trên đường đặc trưng nên có ví dụ Tikhonov về tính không duy nhất nghiệm.
Ngoài ra khi giải ngược thời gian cho phương trình truyền nhiệt thì tính ổn định bị phá vỡ. Bài toán không đặt chỉnh này được quan tâm khá nhiều.
Hôm nay tôi đã hoàn thành việc trình bày phương trình Laplace:
– ước lượng tiên nghiệm,
– nói qua về khử kỳ dị (các bạn tự đọc),
– kỹ thuật Bernstein: để đánh giá gradient và đưa ra bất đẳng thức Harnack dạng vi phân,
– phương pháp Perron giải bài toán biên Dirichlet cho phương trình Laplace,
– nói qua về phương trình Poisson và thế vị Newton.
Hôm nay tôi nhắc lại về thế vị Newton và một số ý liên quan. Sau đó tôi bắt đầu chuyển sang phương trình truyền nhiệt:
– Biến đổi Fourier.
– Nghiệm cơ bản: nhân nhiệt hay nhân Weierstrass-Gauss.
– Nghiệm của bài toán giá trị ban đầu trong toàn không gian với điều kiện ban đầu thích hợp.
– Một vài ví dụ: ví dụ Tikhonov về tính không duy nhất của bài toán Cauchy, ví dụ về tính không ổn định của việc giải ngược thời gian phương trình truyền nhiệt.
– Bắt đầu chuyển sang tính chính quy của nghiệm phương trình truyền nhiệt.
Hôm nay tôi sử dụng công thức dạng DIV để chứng minh:
– tính trơn, đánh giá gradient cho nghiệm phương trình truyền nhiệt,
– tính chất giá trị trung bình trong hình cầu nhiệt và trên mặt cầu nhiệt.
Sau đó tôi chuyển sang nguyên lý cực đại yếu trong miền bị chặn và trong toàn không gian.
Tuần tới tôi cố gắng trình bày xong phần phương trình truyền nhiệt:
– nguyên lý cực đại mạnh,
– đánh giá tiên nghiệm,
– kỹ thuật Bernstein,
– phương trình không thuần nhất.
Các bạn chuẩn bị các bài tập lý thuyết và bài tập giải bài toán biên cho phương trình Laplace. Cuối giờ ta sẽ chữa.
Bài giảng về phương trình truyền nhiệt tôi đã sửa lại và bổ sung thêm
Phương trình truyền nhiệt
Hôm nay tôi kết thúc việc trình bày phần phương trình truyền nhiệt. Tuần sau tôi sẽ trình bày phương trình truyền sóng. Tài liệu phần này:
Phương trình truyền sóng
Hôm qua một số bạn lên chữa bài tập về việc giải bài toán biên cho phương trình Laplace:
– Trong hình chữ nhật, nửa giải:
+B1: tìm tất cả các nghiệm dạng tách biến không tầm thường thỏa mãn phương trình và các điều kiện biên thuần nhất. Với trường hợp nửa dải cần thêm điều kiện bị chặn.
+B2: lập chuỗi nghiệm.
+B3: tính hệ số của chuỗi nghiệm nhờ điều kiện không thuần nhất còn lại.
– Trong quạt:
+B1: chuyển sang hệ tọa độ cực, viết lại phương trình và các điều kiện biên trong hệ tọa độ cực.
+B2, B3 giống trên. Chú ý ở B2 có tính huống bị chặn tại gốc.
+B4 chuyển về hệ tọa độ Decartes.
Các bạn chuẩn bị thêm các bài về phương trình Poisson
Việc giải bằng phương pháp tách biến gần giống như giải bài 2 đề 3 thi giữa kỳ.
Bạn Ngà chữa bài về đa thức điều hòa thuần nhất (homogeneous harmonic polynomials) trong mặt phẳng. Trong khi tính toán nó liên quan đến hàm điều hòa cầu (Spherical harmonics). Các bạn tham khảo thêm
Hàm điều hòa cầu – Đa thức điều hòa thuần nhất
Trước đó bạn Ngà có hỏi về số chiều của không gian nghiệm của phương trình vi phân thường tuyến tính cấp n. Bạn có thể tham khảo
Linear ODEs
Em cảm ơn thầy nhiều ạ.
Câu hỏi ôn tập thi cuối kỳ PTĐHR:
I. Phương trình Laplace:
1. Phát biểu và chứng minh các công thức Green và đồng nhất thức Green. Từ đó dẫn đến tính trơn của hàm điều hòa.
2. Các cách dẫn đến đánh giá gradient. Từ đánh giá gradient chứng minh định lý Liouville.
3. Phát biểu tính chất giá trị trung bình.
4. Phát biểu và chứng minh các nguyên lý cực đại (yếu+mạnh), nguyên lý so sánh. Từ đó chứng minh đánh giá tiên nghiệm.
5. Định nghĩa hàm điều hòa dưới và điều hòa trên. Phát biểu và chứng minh các định nghĩa tương đương.
II. Phương trình truyền nhiệt:
1. Xây dựng nghiệm cơ bản. Từ đó xây dựng và chứng minh nghiệm của bài toán Cauchy cho phương trình truyền nhiệt trên toàn không gian.
2. Phát biểu và chứng minh tính trơn của nghiệm của phương trình truyền nhiệt.
3. Các cách dẫn đến đánh giá gradient.
4. Phát biểu tính chất giá trị trung bình.
5. Phát biểu và chứng minh các nguyên lý cực đại (yếu+mạnh), nguyên lý so sánh. Từ đó chứng minh đánh giá tiên nghiệm.
III. Phương trình truyền sóng:
1. Chứng minh trung bình cầu của nghiệm phương trình truyền sóng thỏa mãn phương trình Euler-Poisson-Darboux.
2. Xây dựng và chứng minh công thức nghiệm Kirchoff (n=3).
3. Sử dụng phương pháp hạ thấp số chiều và công thức Kirchoff xây dựng nghiệm Poisson (n=2).
4. Xây dựng và chứng minh công thức nghiệm trường hợp không gian số chiều lẻ. Từ đó dùng phương pháp hạ thấp xây dựng nghiệm trường hợp không gian số chiều chẵn.
5. Phát biểu và chứng minh đánh giá năng lượng.
thưa thầy! đề cương thầy cho là cm nguyên lý cực đại yếu. vậy là nguyên lý cực đại yếu cho hàm điều hòa dưới hay là cm nguyên lý cực đại yếu cho nghiệm dưới ạ?
Cả hai. Hàm điều hoà dưới là trường hợp riêng của nghiệm dưới. Kết quả cho nghiệm yếu không tốt bằng kết quả cho hàm điều hoà dưới.
Một bạn có hỏi về công thức Green trong sách thầy Hợp. Tôi xem lại thì thấy:
– thầy Hợp trình bày trong trường hợp 3-chiều,
– biểu diễn tích phân trong sách thầy Hợp chính là đồng nhất thức Green trong trường hợp 3-chiều.
Như vậy nếu trình bày như sách thầy Hợp thì chưa đủ cho câu hỏi ôn tập vì chỉ mới trong 3-chiều.
Hôm qua một số bạn chữa các bài tập lý thuyết:
– Bài về các giá trị riêng của toán tử Laplace trong hình chữ nhật![[0, \pi]\times[0, 2\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C+%5Cpi%5D%5Ctimes%5B0%2C+2%5Cpi%5D&bg=ffffff&fg=444444&s=0&c=20201002) với điều kiện biên Dirichlet bằng 0:
với điều kiện biên Dirichlet bằng 0:
+ một bạn tìm các nghiệm tách biến không tầm thường,
+ bạn Tài dùng tích phân chỉ ra không là giá trị riêng,
không là giá trị riêng,
+ bạn Ngà nghĩ đến cách dùng nguyên lý cực đại khi h=0 (trong giáo trình tôi có dùng cách này, cụ thể Định lý 1.22).
Về bài này còn có câu hỏi: Ngoài các giá trị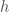 bài toán có nghiệm tách biến không tầm thường, còn có
bài toán có nghiệm tách biến không tầm thường, còn có 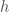 dương nào khác sao cho bài toán có nghiệm không tầm thường không?
dương nào khác sao cho bài toán có nghiệm không tầm thường không?
– Bài chứng minh bất đẳng thức Harnack bằng cách dùng công thức Poisson và tính chất trung bình.
– Bài chứng minh tính điều hòa của hàm khả vi liên tục đến cấp 2 trong tập mở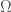 thỏa mãn tích phân trên mặt kín
thỏa mãn tích phân trên mặt kín  của đạo hàm theo pháp tuyến trên
của đạo hàm theo pháp tuyến trên 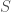 của hàm đã cho đều bằng 0.
của hàm đã cho đều bằng 0.
Ngoài ra một số bạn chữa bài tập về phương trình truyền sóng, phương trình Poisson.
Để giải bài toán Cauchy cho phương trình truyền sóng
với điều kiện Cauchy
ta dùng sóng tiến
và sóng lùi
có
Một trong những bước khó là tính “nguyên hàm”
Dùng cách này ta có thể:
– vẽ tại một số thời điểm
tại một số thời điểm  bằng cách dịch trái sóng lùi và dịch phải sóng tiến,
bằng cách dịch trái sóng lùi và dịch phải sóng tiến,
– xác định được các điểm mà nghiệm kỳ dị, nghĩa là không khả vi đến cấp 2.
Chẳng hạn với hai bài hôm qua chữa trên lớp có hình vẽ:
B1:
B2:
Để vẽ các hình trên tôi dùng Maple:
Các bạn thử trả lời xem các điểm kỳ dị của nghiệm trong hai bài trên là những điểm nào?
Bài 2 còn việc giải u(x, t). Bạn chữa bài này chia thành 6 trường hợp. Tôi đã chỉ ra 3 trường hợp bằng 0. Hôm tới bạn nào tiếp tục chữa bài này.
Bài tập về phương trình Poisson
khi chuyển sang hệ tọa độ cực ta có công thức nghiệm
Công thức này “bắt chước” cách biến thiên hằng số của phương trình vi phân thường.
Thay vào phương trình ta có hệ các phương trình
Thay vào điều kiện biên ta có
Còn cách khác dùng hàm khử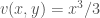 có
có 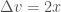 nên khi đặt
nên khi đặt  có
có
Các bạn thử giải bài toán trên khi phương trình được thay bởi
thưa thầy! e muốn gửi ảnh cho thầy xem giúp e làm đúng k! thì e gửi như thế nào ạ? e có thể gửi mail dc k ạ? e cám ơn thầy
Tốt nhất em viết các bước làm chính và kết quả lên đây.
e làm đề cuối kỳ 2015-2017 . pt utt-4uxx=0 với u(x;0)=-1 0<x<1 ; ut(x,0)=1 0<x<1
tìm sóng tiến sóng lùi. F(x)= -1/2-1/4x với 0<x<1 ; -3/4< x< 1
sóng lùi: G(x)= -1/2+1/4x 0<x<1 ; -1/4 với x1
phần b) vẽ tại t=1/4, 1/2, 3/4 ( thầy gửi cho e hình vẽ tham khảo dc k a) e cám ơn thầy nhiều
Bài này cần thác triển lẻ, tuần hoàn chu kỳ 2 các điều kiện ban đầu. Sau đó ta mới xác định được sóng tiến-lùi trên toàn trục số.
e làm đề cuối kỳ 2015-2017 . pt utt-4uxx=0 với u(x;0)=-1 0<x<1 ; ut(x,0)=1 0<x<1
tìm sóng tiến sóng lùi. F(x)= -1/2-1/4x với 0<x<1 ;
-3/4 x1
sóng lùi: G(x)= -1/2+1/4x 0<x<1 ;
-1/4 với x1
phần b) vẽ tại t=1/4, 1/2, 3/4 . e vẽ F(x), G(x). rồi F(x-1); G(x+1) bằng cách dịch sang phải sang trái 1 đơn vị. vậy u(x,1/4) được vẽ như thế nào ạ? e chưa hiểu khi dịch chuyển đồ thị thì suy ra u(x,t) như nào ạ
( thầy gửi cho e hình vẽ tham khảo dc k a) e cám ơn thầy nhiều
Thác triển trạng thái ban đầu:
Thác triển vận tốc ban đầu:
“Nguyên hàm” của thác triển vận tốc ban đầu
Sóng tiến (đỏ) – sóng lùi (xanh)
Vẽ u(x, t) khi t=1/4, 1/2. 3/4:
Từ dưới lên: đường xanh lùi sang trái 2*1/4=1/2 đơn vị, còn đường đỏ tiến lên 1/2 đơn vị. Khi đó u là trung bình cộng đường xanh và đỏ (chỉ tính trong [0, 1]).
Hình ảnh dao động sợi dây
Hôm nay tôi đã trình bày:
– thiết lập phương trình Euler-Poisson-Darboux,
– dùng phương trình trên giải bài toán Cauchy cho phương trình truyền sóng trong 3- chiều không gian, cụ thể thiết lập công thức Kirchhoff,
– dùng cách hạ thấp số chiều thiết lập công thức Poisson,
– dùng bổ đề tính toán giải khi số chiều không gian lẻ.
Các bạn tự đọc:
– một số tính chất nghiệm trường hợp 1, 2, 3 chiều không gian,
– thiết lập công thức nghiệm khi số chiều không gian chẵn,
– chứng minh các công thức nghiệm thực sự là nghiêm,
– tính chất toàn cục của nghiệm.
Phần còn lại tôi trình bày:
– nguyên lý Duhamel,
– đánh giá năng lượng
trong tiết đầu tuần sau.
Tuần sau tôi sẽ tổng kết điểm giữa kỳ.
Tôi vừa sửa lại một số lỗi trong bài giảng về phương trình truyền sóng:
Phương trình truyền sóng
Hôm nay tôi đã kết thúc môn học PTĐHR. Trong tuần này tôi sẽ nộp bảng điểm và đề cuối kỳ lên VPK. Nếu lớp cần bản sao bảng điểm giữa kỳ thì sáng thứ Năm này tôi dạy hai tiết đầu các bạn có thể đến lấy.
Tôi đã đưa bản sao bảng điểm giữa kỳ cho bạn Tài, bảng điểm giữa kỳ gốc và đề thi cuối kỳ cho cô Thúy VPK.
Em chào thầy,
Thầy hướng dẫn em làm câu 1 đề cương phần phương trình truyền nhiệt, cách xây dựng và chứng minh nghiệm của bài toán Cauchy cho pt truyền nhiệt cho toàn không gian với ạ. Vì theo em hiểu thì mình sẽ xét pt truyền nhiệt trong R^nxR, khi đó điều kiện Cauchy cũng phải khác đi gần giống như ví dụ Tikhonov xét pt truyền nhiệt 1 chiều như trong tài liệu thầy cho chúng em. Còn trong R^n thì em không biết phải làm tn ạ.
Thầy hướng dẫn em với ạ. Em cảm ơn thầy!
Xây dựng nghiệm: ví dụ 1.7.
Chứng minh: định lý 1.4.
Em cảm ơn thầy ạ.
Dạ thưa thầy, thầy cho em hỏi câu ly thuyết nguyên lý so sánh phần phuong trinh laplace và phuong trình truyền nhiệt ạ. Em cám ơn thầy ạ
Em có thể nói rõ hơn em hỏi gì về nguyên lý so sánh không? Nguyên lý so sánh nói nôm na muốn so sánh nghiệm từ việc so sánh nghiệm trên biên. Nó có thể như nguyên lý cực đại yếu được viết dạng khác.
E không tìm thấy nguyên lý so sánh trong phuong trình truyền nhiệt và phuong trình laplace là nguyên lý nào ạ, thầy chỉ giúp em với ạ. Em cám ơn thầy ạ
Kết quả nào có việc so sánh giữa u và v là nguyên lý so sánh.
Dạ vâng, em cảm ơn thầy ạ.
Em thưa thầy, trang 35, khi tính đạo hàm theo t của thành phần thứ n+1 trường F, hình như còn có cả a_t nữa chứ ạ.
Trong bài giảng về phương trình truyền sóng, đúng vậy. Tôi đang định sửa lại chỗ đó. Trong trường hợp a chỉ phụ thuộc x thì chỗ đó ổn.
Click to access dethigiuakyk58an2.pdf
Em thưa thầy, ở câu 2 trong đề trên, sau khi thác triển lẻ hàm g thành hàm g* và tính tích phân trên đoạn [-1,1] của hàm g* thì kqua =2 khác 0. Suy ra sóng tiến ,sóng lùi F(x), G(x) không tuần hoàn với chu kì 2. Thầy nói lại giúp em nếu F(x),G(x) không tuần hoàn với chu kì 2, thì sau mỗi chu kì đồ thị của nó thay đổi như thế nào ạ?
Em cảm ơn thầy.
Sau mỗi chu kỳ “nguyên hàm”
sẽ thêm vào đúng một tích lũy trong một chu kỳ
Cụ thể, với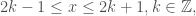 có
có
Vâng ạ. Em cảm ơn thầy!
Tích phân của hảm lẻ trên [-1, 1] bằng 0!
Vâng ạ. Em nhầm chỗ này ạ. Em cảm ơn thầy!!
Thưa thầy, thầy cho e hỏi câu phát biểu và chứng minh đánh giá năng lượng( trong phương trình truyền sóng) là định lý nào ạ?????, em cám ơn thầy ạ.
Chính là các kết quả tôi trình bày ở buổi học cuối cùng. Những câu hỏi điển hình cho việc chữ thầy trả thầy.
Dạ vâng, em tìm thấy rồi ạ. Thầy cho e hỏi trong bài 3( xét bài toán biên cho phuong trình laplace trong quạt). Đề thi học kì k59 tài năng ạ, có u(x,y) = min{x,y} khi x^2 +y^2 = 1; với điều kiện như này thì xử lý thế nào ạ?????. Em cám ơn thầy ạ
Khi chuyển về hệ tọa độ cực xem góc như nào thì bằng x, góc như nào thì bằng y?
Dạ vâng, em cám ơn thầy ạ
Thưa thầy cho em hỏi trong hình cầu thuộc không gian n chiều thì dS , dSy là gì . Nó được tính theo công thức nào? Vì sao khi đặt y = x+pw thì dSy=p^n-1 .dSw. Em cảm ơn thầy ạ
Chẳng hạn n=3 thì dS hay dS_y là vi phân mặt. Việc tính bằng cách nào phụ thuộc việc tham số hóa mặt cong mà ta tích phân trên đó. Chẳng hạn ta lấy mặt cong là mặt cầu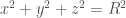 được tham số hóa bằng hệ tọa độ cầu
được tham số hóa bằng hệ tọa độ cầu  thì
thì
Khi đổi biến có “Jacobien” là
có “Jacobien” là 